 |
Dynamics of Complex Waves |
| A.G.Booth | Original on WWW 6 February 2005 | Copyright © A.G.Booth 2005 All rights reserved | ||
| Document ident: | Last updated 1 September 2005 | Dynamics of Complex Waves. A.G.Booth | ||
Keys: |
quantize quantized quantization wave equation continuum theory |
|||
This document makes use of the HTML character entities in its text, so if your browser does not support them you will see the raw HTML tags that call them up. Preferred browser is Firefox, but I believe that the text should display adequately for versions starting from v4.5 for Internet Explorer, v6 for Netscape and v6 for Opera. There are .PDF files offered to ease this problem.
 Contents
Contents
- Introduction and Motivation
- Note on Vectors and Tensors
- Simplest Possible Equation
- Singularities and Interactions
- Superposed Stochastic Waves
- Building the Interactions
- Electromagnetics
- Electrodynamics
- Scaling the Fields
- Nuclear Dynamics
- Gravity
- Conclusions
- Appendices
- Acknowledgements
- References and Background Reading
This symbol denotes linkage to an independent web site:
The "Document ident" shown just below the header of the paper and showing date of last update should be used to check for the specific form of the paper, in cases where that might matter. Please communicate comments to Tony Booth.
 Summary
Summary
The zero d'Alembertian wave equation has a particularly simple structure. With the added stipulation of rotational symmetry of interactions to comply with the Euclidean nature of our physical 3-space and the presence of an endemic noise field the model gives rise to behaviour corresponding to many natural physical phenomena. The picture is developed by applying stochastic correlation analysis to a complex scalar noise field in the Minkowski 4-space. The results are developed by following these steps:
- Discuss the zero d'Alembertian complex scalar wave model with its waves at speed of light.
- Link its singularities with spin and postulate a set of slower eigenmodes supported by noise.
- Analyse the combined field in terms of its correlations and spectra by Wiener methods.
- Separate the coupling terms to correspond to the conventionally recognised physical forces.
- Use these couplings to build dispersive wave models (Klein-Gordon or Schrödinger equations).
 Introduction and Motivation
Introduction and Motivation
Whilst thinking about engineering wave models as candidates suitable for use in electrodynamics the following structure of dynamics arising from a very simple initial model became apparent. The ideas moved something like this:
Occam's Razor
The existence of the same constant (the speed of light) appearing in two structurally distinct dynamic systems (Maxwellian and De Broglie waves) in our models of natural dynamics is enough to arouse the parsimonious sense of Occam's Razor in us. It leads us to suspect that there must be some supervening common model. Further, just looking at the form of the Klein-Gordon or Schrödinger equation and wondering about its constant term in the operator (the one that causes dispersion of wave velocity) suggests gravitational mechanisms through induced phase tilts by making its value a function of spatial position. Here then is, perhaps, a path to the supervening model. Can an underlying field with simple structure embrace both of these wave models (Maxwell and De Broglie) whilst manifesting the properties we observe in physics?
The search went like this:
Einsteins's gravitational light bending trick is right.
My own wave model estimate of Sommerfeld's fine structure constant is on the high side.
So substrate spectrum and/or velocity range might be "sub-light-cone" in order to get coupling, but as developed hereunder that looks unlikely. Rather the involvement of singularities (in the nature of spin) may be key. Still some form of finite intensity field may be involved. From prediction errors for the fine structure constant or some other marginal effects we may then be able to deduce this coupling margin, and interpret it into nuclear mechanics to produce the value of the neutron mass.
For greatest simplicity we need reasoning, if possible, to show that there are not two independent functions, one spectral and the other velocity distribution, in determining the nature of this substrate field.
Time survives as a reference parameter
In studying correlations in a wave field we do not necessarily have to think of cross correlation functions between first derivatives as referred to translations of their respective dimensional co-ordinates. Rather we can form correlations always over time as the correlation parameter between each pair of local partial derivatives in the four space. Then the resulting 16 element correlation matrix can be converted to a hybrid frequency domain form by taking the Fourier transform, over the domain of its time parameter, of each of its element correlation functions.
In its unique position as contrary to the three Euclidean dimensions time serves to take on the negative characteristic in the second differential, and hence develops the steady oscillatory nature that gives it long term correlation/persistence, unlike the Euclidean relationships amongst the spatial dimensions.
Substrate noise would seem to enter the dynamics model only in the effect of its fluctuation variances and correlations, and that is at a level of modelling much lower than the uncertainties associated with quanta (at least, it is at the lower frequencies). This is more than merely a matter of zero point fluctuation entering the dynamics at the first hand by being there in the Maxwell field.
 Note on Vectors and Tensors
Note on Vectors and Tensors
The star symbol as in x* denotes complex conjugation.
Matrices and vectors are set in bold sans-serif type ... scalars: x, X, ξ, Φ vectors/matrices: x, X, ξ, Φ.
Symbol T as in XT denotes vector or matrix transpose. An untransposed vector is a column, though
in the line of text may have its elements depicted horizontally.
A direct (Cartesian) product of two vectors could be depicted as a column vector pre-multiplying a row,
e.g. in A.BT, but will alternatively use the special symbol for the direct product as in A B .
B .
Also symbols  and the pair
and the pair 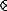
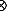 will be introduced below for handling direct products of vectors and inner products of matrices.
will be introduced below for handling direct products of vectors and inner products of matrices.
The dagger symbol as in X† denotes adjugate matrix, i.e. the matrix of signed minors (not yet used herein).
The copyright symbol used as a binary operator as in A©B denotes the convolution operation (not yet used herein).
Vector Differential Operators:
Many issues herein could be expressed very compactly in tensor notation, but our mission here is topological comprehensibility and not conciseness or mathematical generality for its own sake. Instead I shall mostly adhere to the layman's sense of distinctness between time and space and treat the co-ordinates as a compound
Such a
Thus the separation into time as a scalar real variable and space as a
Because we need to use both four dimensional expressions as basic definitions and three dimensional expressions where static approximations occur we need to make sense of the distinction between the respective differential operators. First we combine the 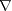 differentiations into a single four dimensional operator denoted by the lozenge symbol ◊. I avoid here the square symbol
differentiations into a single four dimensional operator denoted by the lozenge symbol ◊. I avoid here the square symbol  called "box" or "squabla" because elsewhere, at least sometimes, it is used to represent specifically the Minkowski four dimensional second order differential operator ... the d'Alembertian. By embedding constants in this ◊ operator (and, indeed, also in D,
called "box" or "squabla" because elsewhere, at least sometimes, it is used to represent specifically the Minkowski four dimensional second order differential operator ... the d'Alembertian. By embedding constants in this ◊ operator (and, indeed, also in D, 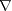 and the generalised frequency
and the generalised frequency
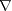 ] { ≡ τC [∂/∂t, c.∂/∂x, c.∂/∂y, c.∂/∂z]in practical units} ] { ≡ τC [∂/∂t, c.∂/∂x, c.∂/∂y, c.∂/∂z]in practical units} |
Eloz |
Using this symbolism the second order Minkowski differential operator (the d'Alembertian) can be written as  ≡ ◊T·M·◊
≡ ◊T·M·◊
|
Emink |
For cases where we wish to analyse a system that can be described as linear with constant or perhaps very slowly varying parameters then to achieve improved separability of its dynamic terms we shall wish to express it in terms of the frequency domain transform of its wave variable. Thus a complex wave variable
In the case of slowly changing linear systems then the system dynamic coupling coefficients can be treated as being slowly varying functions of time, and the analysis can follow as a slowly perturbed result derived from the steady state behaviour. The restriction to "steady state" includes the cases of multiple modes each in steady oscillatory motion. The question of how slow is "slow change" then rests upon whether the (eigenvalue) variable
Hybrid Differential Operators:
To allow expressions corresponding to differentials treated symmetrically over space and time (as is typically done in relativistic considerations), but using the frequency domain for the time dimension, we shall need a hybrid form of the differential operator. Thus a frequency domain hybrid lozenge operator
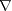 ] { ≡ τC [s, c.∂/∂x, c.∂/∂y, c.∂/∂z]in practical units} ] { ≡ τC [s, c.∂/∂x, c.∂/∂y, c.∂/∂z]in practical units} |
ElozF |
In this hybrid operator the first element operates multiplicatively upon the elements of left or right entities whilst the remaining differential elements operate each as though convolved with elements of its operand that is the neighbouring entity immediately to its right. In this latter respect we consider a differential here to be the integral of the operand weighted by a smooth doublet function centred around the given co-ordinate value, with unit moment, that is then taken sufficiently close to its narrow limit to be valid. So the first element of the hybrid operator commutes with operators or functions to left or right, but the differential operator element, although in succession of differentiations still commutative over the same or anti-commutative (sign reversal) over different independent variables, cannot commute with functions of the variable of differentiation either to its left or to its right.
 Simplest Possible Equation
Simplest Possible Equation
In the study of wave systems in physical space we may write a generalised form of the complex scalar Klein-Gordon partial differential equation with added coupling terms in both the space-space and the mixed space-time derivatives as:
| Ekg |
Study of the model generated by this second order differential equation and its somewhat less general first order cousin the Schrödinger equation leads to properties in the solutions that correspond valuably to the phenomena we observe around us that we classify as "electrodynamics". That is discussed and demonstrated in an accompanying essay Smooth and Quantal Properties of the Complex Wave.
Here the exploration is taken to a lower level of causal processes based upon an even simpler wave model.
Given that we appear to get fruitful results from the kinds of models cast in the form of a complex variable that is a function of position in physical space, we might ask what is the simplest constraint on mathematical good behaviour of such a function and see how useful that might be. We quickly arrive at the desirability for some sort of smoothness in the function, in particular that it should not have precipitous sharp steps with infinite gradient anywhere. This idea is motivated as part of the wish to allow causality to work always locally. If the rules for such local relationship are to remain as simple as possible then this sort of smoothness can make mathematical and rational life a lot easier to lead.
A very simple form of constraint rule is to equate the sum of the second partial derivatives to zero. You might be tempted by the even simpler first order differential constraint, but its only solutions are flat ... too boring.
So we take up the second order option, but there is a tricky bit about this in that we are permitted either sign for the terms in this summation of second derivatives. The arrangement that seems to fit our requirements best gives a reversed sign to that term for the time dimension. If we did not do this time would be part of our static geometry (Pythagoras' theorem would work symmetrically in all four dimensions), and we know anyway that it does not do that. Having this sign reversal present produces what we talk of as a wave equation (it has solutions that are wave-like). The geometry that results from this sign reversal of the time related second order term is attributed to Minkowski, and we therefore talk of this as the four dimensional Minkowski space. It is the basis of special relativity.
Thus the simple arrangement of equating this form of second derivative of the complex scalar variable to zero presents itself as about the simplest basis for a causal model we could wish for. This essay explores the forms of solutions of that equation, though we shall also consider the effects of allowing certain well behaved singularities to enter the game too. By "well behaved" here I mean that these singularities are still limited to finite squared magnitude, which along with a finite temporal frequency means finite energy density. In fact, since the restriction applies jointly across the four dimensions including time we may regard this restriction as a finite action density, action being measured in units of energy multiplied by time. These singularities break up the monotony of an otherwise totally smooth solution and, as we shall see, by seeding the structure of spin they make possible the existence of matter.
This sum of the second derivatives over the four dimensions with sign of the time element reversed is given the name "the d'Alembertian", and is traditionally denoted by  , a symbol referred to variously as "square", "box" or "squabla".
, a symbol referred to variously as "square", "box" or "squabla".
So the most basic form of the equation constituting dynamic complex waves in three physical dimensions consists of nothing but the d'Alembertian operation on the scalar complex wave function equated to zero which we may write in the appealingly compact form of  ψ = 0
ψ = 0
| ◊T·M·◊ ψ(t, x) = 0 | EZdA |
It is true that for this equation there is a set of solutions in plane waves that spans any physical Euclidian 3-space in our Minkowski 4-space, and all of these solutions imply four dimensional solutions (by extension under the zero d'Alembertian) that have the same characteristic speed (speed of light). These waves are all mutually orthogonal, they do not interact with each other at all. The general form of such a single plane wave with amplitude α, angular frequency β, 3-vector direction ζ and phase γ may be expressed as:
| ψ(t, x) = α.cis(β[−1, ζ]T.[t, x] + γ) where |ζ| = 1 | Enat |
I shall refer to this three dimensional set of four dimensional wave solutions below as the "native" set. They have the nature of a complex Fourier basis for a continuous space of three dimensions. Because of the conical 4-space geometry of the vector directions of these native waves they are said to exist "in the light cone".
What we shall think of as the "power density" of these waves is proportional to the squared magnitude of the first derivative, not to the squared magnitude itself. On this basis, if we wish to form the total energy of a set of waves with different frequencies by summing their squared magnitudes then each such square must be multiplied by the square of its corresponding frequency.
There is an alternative transformation of this native basis set into the set of all radial waves with magnitude asymptotically inversely proportional to distance from a given centre point and with radial speed equal to the speed of light. The elements of this basis each have a finite maximum magnitude at the centre, and for a given magnitude asymptote at great distance this central maximum has a magnitude that is proportional to the frequency. Alternatively, for a given distant field time derivative magnitude the amplitude at the centre is independent of frequency, but still the central maximum always has a width that is inversely proportional to frequency. The phase velocity of these radial waves is also in the light cone as were the plane waves mentioned above, but there are some difficulties in interpreting phase velocity proximate to the centre of the radial pattern.
These waves so far described correspond closely to those used by both Milo Wolff and Chris Hawkings in their respective discussions of modelling matter by means of waves. Those authors present descriptions of matter based upon wave structures. Here the picture of the waves will be taken further by introducing the rôle of singularities as means to obtain interactions before seeking the forms of solutions. That way the wave structures are not merely described but emerge as naturally produced solutions of the wave model equations. They are shown as having natural forms and frequencies and natural levels of amplitude. Also the set of wave function structures produced this way is richer in detail, as it will transpire.
 Singularities and Interactions
Singularities and Interactions
Both the plane wave basis and this radial basis set of waves span the same three dimensional space, so either may be used for forming finite three dimensional integrals that are stochastic (i.e. summed over random or incoherent sets). So both the plane and radial forms of this (native) Fourier basis can form valid integrals as wave functions (both, of course, because they are equivalent bases) so long as the sum of the squared derivative (i.e. total energy density) is finite. This amounts to their having finite spectral density and bandwidth. But we still have no mechanism of interaction between the elements of this set of waves in either of its forms.
To achieve interaction it is necessary to introduce a special kind of wave function that from the outset relies for its existence upon interaction. Such a wave can be constructed from components that would each alone violate the defining wave equation (and therefore could not exist individually), but when taken together cancel their illegal effects. In these particular cases of combination a persistent wave may exist, but only when in addition it produces the scattering of a background field of noise-like plane waves. Scattering corresponds to converting waves of the plane kind to those of the radially propagating kind. Such combination waves are not of themselves solutions of the original wave equation, but so long as the scattering they cause has certain stochastic equilibrium properties then these special additional forms of waves can exist in persistent forms. By this means interactive processes can arise in this complex scalar wave system on Minkowski space. Any of the simpler systems of scalar waves that are real and/or on Euclidean space cannot produce these properties.
(One might be tempted to conjecture the existence of further more complicated interactive extensions to sets of wave solutions on Minkowski-like spaces of sufficient dimension over quaternion or octonian scalar variables ... I wonder!)
It is as though a kind of boundary effect on stochastic eigen functions can exist as distributed throughout the physical space (rather than being independently defined by some bounding surface). Also where these terms persist so they can mediate alternative overall solutions in that they scatter the waves of the native system. It turns out that these additional terms are necessarily bound up with the possibility of "spin" topology (the native set are all spinless), and where they exist at all they display the tendency to settle into fluctuations around discrete attractor states.
Let us refer to this stochastically based extension of the set of solutions of the zero d'Alembertian rule as the "derived" set.
There is no mutual interaction between waves in the native set (at least almost none, c.f. the gravitational light bending effects demonstrated by Einstein ... we must also ask "Does light gravitationally attract light?", so there remains a question regarding the exact truth of this statement, at least physically even if not mathematically), but this is not true of waves in the derived set which interact strongly (consider van der Waals forces). Also the native waves are not generally orthogonal to the derived waves, and therefore interactions are possible between element pairs with one each from the native and derived sets. Indeed, without this interaction the derived set could not exist at all ... alone they cannot maintain equilibrium as solutions of the zero d'Alembertian wave equation. Presumably it is for this reason that I find they are omitted in the usual mathematical descriptions of the solutions of this basic wave equation (still searching for refs!). It also transpires that there is no such derived set of wave solutions if the wave variable is real; it is only possible for the necessary structures to exist with a complex variable.
From these two classes of solutions we can begin to see the emergence of the distinction between the Maxwellian phenomena (as waves at speed of light) and the De Broglie phenomena (where geometric mean of phase and group velocities is speed of light). However, neither the Maxwellian nor the De Broglie waves can be directly manifested as the wave processes I have been describing. The De Broglie waves are indeed the derived set, but for these to exist there must be a background field of native waves present. This background field of native waves must occupy a broad band of frequencies and I shall call it the "substrate field". As for the Maxwellian phenomena, these vector waves are realised as correlations amongst the native plane scalar wave elements of the substrate field. In free space (with native waves only ... no matter present), as a result of the total absence of interactions amongst native waves, these correlations decay in intensity according to the inverse square law of distance. Again, such correlations could not exist unless there were a substrate field to support them.
We need to understand how the native and derived waves might interact, in spite of the wave equation being linear in the sense of the terms in the equation all being of only first degree in the wave variable and its derivatives. The only prospect then is to uncover some sort of interaction based upon a singularity at the centre of a spherical wave structure.
For a spherically symmetrical wave field in time plus three spatial dimensions the integral of an inbound linearly superposing wave from a finite spherical symmetric source in space produces only finite values around the spherical centre. The intensity at the central point is finite. Most importantly, the superposed wave components in this system do not interact. So in the absence of any singularity of a simple radial type we are left to look for some other structure as the basis for interactions between plane and spherical wave systems. Thus we turn to the notion of spin structure in the wave fields. We may be tempted to explore the possibility of singularities with infinite densities at the centre but finite integrated energy. However, we shall not even need to go that far ... the spin fields can be constructed around an axial singularity of a line rather than a point type, and that has finite energy density everywhere, and indeed, a zero energy density at the central axis. For further description of the form of the spin singularity please refer to the accompanying essay Wave Topology of a Spin Mode.
That substance shall exist means that it will display its persistent nature. That is its tendency for geometric perturbations to revert by converging to an attractor state. It is necessary that the wave modes comprising it shall have their perturbational damping effected through values of, and particularly by signs of the mixed space-time terms in the respective wave equations. This necessity leads to the universality of the form of the attractor mechanisms, which comprise, at their lowest level, the charge quantisation effects. This fact is common across theories of both electrodynamic and nuclear processes. The opposite signs of these terms produce anti-matter, which is the version of matter with divergent nature ... it has characteristically a repeller point in its nearby state space.
Remarkably, there exist artificial contrivances capable of ushering a limited range of such unstable anti-matter entities towards their respective state repeller points so that they may be stored practically over extended periods of time without direct matter-matter interaction and therefore without the consequent annihilation occurring. For more detail regarding these processes refer to the section "State Attractors" in "Emergence of Quanta in a Wave Model" and also in that document Appendix B.
 Superposed Stochastic Waves
Superposed Stochastic Waves
With spin singularities present the most general solutions to the zero d'Alembertian equation involve interactions, and consequently to model them in full generality is transcendentally complicated. Therefore we must seek a basis of workable approximation that will remain applicable over the range of solutions with which we hope to work. So we start on such a limited basis by seeking separability of terms and factors in the solutions.
Some Mathematical Notes
These notes give an idea of some methods of analysis that may be applied to these correlations, but they will not be developed at length within this essay.
Spectral Averaging and Normalising
There are alternative ways of taking the temporal average for a correlation, and they create different approximations. This is also the case for the forming of Fourier integrals of functions of unbounded time as occurs in this text. The prescription of the autocorrelation function might better be based upon an infinite integral and a smooth weighting function for its definition, the Gaussian
Where necessary herein such finite parameter integration is assumed to operate. Also whereas the integral for a finite duration time series is "all of a piece" and therefore usually energy-like or impulse-like, the corresponding kinds of spectral or correlation integrations used over sections of an infinite duration time series (say like noise) are normalised as averages to be respectively power-like or amplitude-like.
These ideas also tally well with and gain support from the Wiener-Khinchin theorem (effectively, to get from time series to the spectrum, you can either autocorrelate and then Fourier transform or else Fourier transform and then absolute square ... and the same generalisation applies to the bilinear factors that constitute cross-correlations and their associated cross-spectra). To get the benefit of Parseval's theorem (sum of power over spectral frequencies equals sum of power over instants of time) it is necessary to pay attention to normalising the correlation and Fourier transformation averages properly.
Laplace and Generalised Gabor Transforms
A similar approach may be taken with the more general case of defining the Laplace transform, especially if it is thought of as the sum of a cluster of wave elements with fluctuating pole characteristics (i.e. fluctuating eigen values). Rather than using the one sided infinite integrals usual for the Laplace transform we may use a central generator integral based upon a Gaussian weighting function. This produces a generalised Gabor transform. It is generalised in the sense that we may form it for all values of the complex variable rather than restricting it to the imaginary axis of the complex plane as is usual for the Fourier or Gabor transforms.
We may then extend the definition of the transform such that the magnitudes and phases of a modal form are also defined against some "key" phase/frequency reference, invoking a musical analogy. That offers the advantage of analytically handling the relative phases within a given time series in an abstract way for auto as well as for cross correlation. Tessellation of the tempero-physical space, either discretely or on a mathematical limit basis also then offers means for algebraic and computational procedures as per Gabor. Extending the musical analogy, then given a "choir" or "ensemble" of such modal motions we are free to treat the key frequencies of the various modes as independent or common, depending upon their relative dispositions in the frequency space, and then the analysis can follow accordingly. When they can be treated as common (a narrow band choir model) then the analysis becomes concerned essentially with the modulation sidebands.
From an engineering point of view there are advantages to this mathematical scheme in spite of its possibly complicated appearance at the outset. One is that the integration processes are all confined by the presence of the Gaussian function to be well behaved and convergent at high frequencies in a manner controllable by the analyst. This permits an approach to most of the mathematical existence questions on a basis of the tolerancing of model errors, which is a procedure generally familiar and acceptable to engineers. Further, the schemes of computation to which it leads suggest naturally some attractive and powerful ways of improving computational economy such as are widely used in modern signal processing and analysis.
Hybrid Transforms
Above we applied the notion of hybridising the differential operators to accommodate mixed transformed and untransformed elements. Now the idea of hybridisation is extended to the transforms themselves.
Consider a wave mode defined in hybrid terms in the sense of using functions of frequency in the short term and of time in the long term. Consider the function over a region of time-space close to
Using a generalised frequency variable
To extend this method of analysis to cover the case of an ensemble or choir of modes in a band of frequencies that is small compared to the centre frequency we may approximate by replacing the characteristic frequency of each mode with a common key frequency. So long as the analysis is then performed with the time intervals and the Gaussian weighting window of the Gabor transforms limited in time to substantially less than the reciprocal angular frequency bandwidth of the ensemble then accurate results can be achieved whilst confining analysis of the dynamics to the sidebands alone. They are expressed in the term
Classes of Wave Functions
We often consider the class of complex functions on the complex plane (Argand diagram), and restrict ourselves to those defined by rational fractions formed as ratios of polynomials in that complex plane co-ordinate value. These are meromorphic functions, meaning they have singularities but only non-essential ones and only occurring at distinct points. All of these functions are analytic (i.e. having well behaved derivative) except at the singularities (poles) that occur at zeros of the denominator. Furthermore the derivative of such a function at any non-singular point in its complex domain exists as a unique complex scalar, i.e. satisfies the Cauchy-Riemann conditions, which means that at that given point it has the same value regardless of the direction in the plane along which the derivative is evaluated. This set of functions is used widely for analysis of dynamics problems.
In considering solutions of the four dimensional time-space wave equation we shall need a more general set of functions than that, but a set where a sense of analyticity and well-behavedness still remains. And a two dimensional nature in the domain of these functions is still required too. The complex functions are to be expressed more freely such that their domain is a space defined by a set of real variable co-ordinates, and the equivalent of the real and imaginary parts of the more constrained complex number co-ordinate system must be constructed from them. Also although the functions can still be meromorphic it will be necessary to go beyond the set of rational fractions to certain types of transcendental functions with half order singularities.
Because we must allow rotation of co-ordinates in the Euclidean 3-space we shall be particularly interested in those geometries where any plane domain could be considered alternatively in its physically mirror-inverted and hence rotationally reversed form. The term "enantiomorphism" is applied to topological distinctions through reversal by mirror image. The two enantiomorpnic sets of meromorphic functions are indeed distinct because they map oppositely the chiral handedness of circuits in any given domain plane.
Thus by adding terms that are functions taken from these two enantiomorphic sets there can exist derivatives that do not satisfy the Cauchy-Riemann condition of rotational invariance. Instead it is then necessary to consider the sum of two possible functions, one for each rotative orientation of any given plane co-ordinate system. By referring this requirement to any chosen pair of axes in the plane this is equivalent to defining the class of functions as the combination of both the original set of rational fractions and the set of their complex conjugates ... there are twice as many possible functions in the set. This way the Cauchy-Riemann condition applies at each point in the plane only with respect to each of two additive component functions independently. Fortunately this does not necessarily spoil the linear independence of these functions as terms in the solutions of the wave equation, and vital to our purpose here, it does introduce coupling mechanisms associated with singularities. The type of singularity needed to bring this about is of a half power order, so the functions involved are transcendental rather than rational fractions. Also such singularities only ever occur where the function takes zero value.
Thereby begins the account of "spin" and with it the emergence of the persistent waves that generate the properties of matter.
Separability Postulates:
Consider a substrate endemic noise field of native waves
The total field
φTT(τ, x, t) = (1/2A) ∫−AA ((◊ψT*(t + tA − τ/2, x))  (◊TψT(t + tA + τ/2, x))) dtA (◊TψT(t + tA + τ/2, x))) dtA
|
Ecorr |
From symmetries in the definition of the element correlation functions in Ecorr we have
There is a corresponding spectral matrix
| ΦTT(jξ, x, t) = ∫∞ cis(ξτ).φTT(τ, x, t) dτ | EAspect |
The symbol ξ is used here to represent angular frequencies of components of the substrate field, whilst the symbol ω is reserved for the typically much smaller angular frequencies of the derived waves. This is helpful in maintaining clarity when both are appearing in the same formula. The wave functions of the derived field usually occur as eigen functions and their eigen frequencies are therefore discrete and often appear with a suffix as ωn to indicate one particular such frequency for the nth mode.
The symmetries in this spectral formulation are again strong so that for
We may alternatively think of the entire problem in terms of the hybrid frequency domain representation. In that case the basic scalar wave equation, the "zero d'Alembertian" EZdA above, is replaced by a corresponding scalar equation in terms of the Laplace transformed variable where the transformation is made with respect to the time dimension only. These frequency domain variables are denoted here by upper case symbols to distinguish them, and that is similar to the way that the spectral (frequency domain) relationships are distinguished from their corresponding correlative (time domain) relationships. For the general case of the total field the constitutive equation is then:
| ◊jξT·M·◊jξΨ(jξ, x) = 0 | EZhybrid |
We maintain the option to keep time as a further argument placed at the end, as, for example ◊jξΨ(jξ, x, t). This is to allow for non-stationary statistics ... the statistical averages are then formed as centred upon the value of the time argument. For the cases where the statistics can be considered as stationary then the original time argument can be omitted. This means that in the hybrid formulation the frequency replaces time as the first vector element and appears in the function arguments as the first in the list.
Taking advantage of the similarity in form between the correlation integral and a convolution with the time parameter reversed in sign in one of the two factors we may alternatively re-express the correlation spectral result directly in terms of the Fourier transform of the original scalar stochastic wave function (with suitable boundaries to Fourier integration as per the Gabor transform, and normalised to power as commented in the notes on "Averaging and Normalising" above). In these terms the statistics of the wave are summarised in their auto-spectral matrix
ΦTT(jξ, x) = 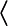 (◊jξΨT*(jξ, x)) (◊jξΨT*(jξ, x))  ◊−jξTΨT(−jξ, x) ◊−jξTΨT(−jξ, x)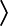
|
EFspect |
The angle brackets around this expression are to convey the need to use some form of averaging or smoothing in the frequency domain in order to avoid pathological degrees of narrow band structure in the spectra produced.
This ill-behaviour in the fine spectral detail is not in fact pathological since these spectral functions ΦTT(jξ, x) will only ever take effect in the form of their integrals over the frequency domain, and those integrals will then converge well enough in the narrow band fine detail. This can be regarded as an issue of Lebesgue integration.
These stochastic matrices are a dimensionally asymmetrical formulation of the statistics with local time as the basis of the frequency transform, a kind of inertially based parameter for the statistics, but with space handled directly rather than in any equivalent sort of wave number transformation. The correlation integrations (of which the possible forms of averaging are not detailed here) are over offsets in time only, not in space. Such an asymmetrical approach is useful, and indeed necessary, because of the special status of the time dimension in the Minkowski geometry.
Because of the quasi-linear nature we are dividing the problem into components that are narrow bands of locally defined temporal frequency, as is typically done in engineering dynamical analysis. It does not invalidate the relativistic requirements (Lorentz invariance) of the resulting analysis so long as any such co-ordinate transformations are performed properly, and anyway, many analyses need no such transformations.
When needing to deal with time varying systems then so long as the rate of variation is slow compared to the bandwidth of ΦTT then the stochastic matrices can also be made functions of time as
A mathematical framework for this combined time/frequency basis of analysis with the necessary rigour can be found in the work by Gabor and to some extent in its more recent developments in wavelet theory, but beyond this mention and the foregoing notes that will not be developed further here. It is however interesting to note in passing that Norbert Wiener, who was the originator of the style of stochastic time series analysis used here, and Dennis Gabor were both cyberneticians ... indeed, it was Wiener that coined the term "cybernetics".
Constraints on Derived Waves:
We seek to account for the way that deterministic waves may display the physical coherence and persistence of matter whilst satisfying the zero d'Alembertian equation, and to that end we invoke the supportive influence of an endemic noise substrate field. Such matter must be capable of moving arbitrarily slowly with respect to our reference co-ordinate system. However, we know that any suitable solution must remain Lorentz invariant and thereby accommodate changes of velocity of co-ordinates, and we expect that to be possible by adhering to second order equation structure (Helmholtz or Klein-Gordon) in any form of approximation we set up. Thus we may confine our attention to proving the existence, that is the physical viability, of static forms of wave modal systems as attractors about which stochastically supported persistent wave processes can centre their fluctuations.
In order that such an attractor may be static requires that the intensity distribution of the wave mode(s) we propose shall stand still in our co-ordinate system. This suggests that the wave mode(s) should have zero group velocity. But we shall also need to include the possibility that there can be a closed and steady circulation of what we think of as charge (i.e. spatial integral of intensity times modal frequencies), and still regard the system as standing still. This steady current circulation is a quasi-dynamic feature forming the origin of magnetic effects. So really for any single mode it is something like the vectorial mean of the intensity weighted group velocity that we need to remain at zero. This corresponds to the idea of a "centre of gravity".
Note here how the complex variable permits at least topologically a steady wave flow with constant intensity at all points ... indeed, without even any group velocity. That is something that cannot be achieved in a Lagrangian model with real variables unless you superpose two part-models and constrain them to a similar complex structure. But by comparison with that the model used here is built more simply, more directly.
For any given wave eigenfunction of magnitude μ and phase angle α we may write down a Stationary Intensity Criterion at any given point, but still allowing circulatory flow of charge, as the rule:
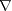 μ(t, x). μ(t, x).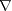 α(t, x) = 0, ∂μ(t, x)/∂t = 0, ∂α(t, x)/∂t = 0 α(t, x) = 0, ∂μ(t, x)/∂t = 0, ∂α(t, x)/∂t = 0
|
Estat |
This rule is not additional to the basic wave equation except in so far that it is essential for persistent existence of any derived field eigenmode. In fact it is not strictly necessary that it shall be accurately fulfilled. Rather it is a rule governing the form of an attractor wave function, whilst the actual wave can fluctuate around that form with small perturbations induced by substrate field interaction over a wide range of frequencies. However, further development and checking of this idea is due in order to deal with the combination of two frequencies involved in a spin based wave mode.
The rule says that for a mode in the steady state its charge is allowed to flow by wave propagation, but only along paths of constant intensity of the said mode (i.e. perpendicular to its local magnitude gradient vector). Whilst this is possible in a complex wave model it cannot happen in the real variable models built on the Lagrangian or Newtonian basis such as with particulate electrons. In these conventional physics models all acceleration of charge causes radiation, so that circulating charge, say like electrons orbiting a nucleus, must radiate energy and thereby collapse to low energy. The wave model makes a different prediction on this as on several other points. These paths of steady state flow can be curved in space yet so long as they comply with this rule there will be no radiation of energy caused by the circulating charge. In order that energy shall be radiated by an individual wave mode acting alone it is necessary for either the paths of such flow or the locations of the wave intensity to undergo accelerative change. The smooth sort of circulatory motion of which complex waves are capable is not a basis for such radiation. More will be said about this below when the nature of propagative field induction has been further developed. Our task remains to set up the reasoning that field components satisfying this criterion of persistence can exist.
This rule requires that charge flow shall always be spatially orthogonal to any gradient of magnitude. For some reason (find this reason!) this rule can only be satisfied by solutions with paired frequencies of which the following factor wave function is an example:
We may note that low pressure acoustic waves in a non-flowing inviscid fluid obey the same form of zero d'Alembertian scalar equation for their dynamics (exclude solids as such a model because of the additional effects of shear and rotative forces). In that acoustic model plane waves propagate in a manner similar to the substrate waves discussed here. The puzzle then arises as to why they do not display the full richness of behaviour of the waves considered here including relativistic effects. The difference is that acoustic waves occur with a real variable (consider pressure), and that cannot satisfy the above Stationary Intensity Criterion over flows of wave energy. To go beyond that requires the variable to be complex. This also means that the acoustic system is amenable to analysis under the Lagrangian model, while the system discussed here is not. From that difference arises the possible existence of spin and along with it the enormous extension to the range of solutions that display the properties of substantial matter arising from complex wave structures.
 Building the Interactions
Building the Interactions
The correlations and also the spectra of the field are bilinear functions of the gradients ... they are actually direct products of gradient vectors. Thus by applying a divergence operation we can bring into existence the form of the original wave equation in each of the two linear factors of the bilinear product, except that each of the linear divergence operations must be compensated for the operation of the other because the wave invariance is only mono-linear. This compensation can be applied in the form of a matrix embedded into the additional bilinear divergence operator. Since the bilinear operations are themselves matrix rather than vector operations we may use a matrix to contain the two vector compensation effects whilst holding these effects independent of each other. We may then use algebra to manipulate the expressions as a whole and to study the cross terms which represent interactions between the various parts of the field.
Primarily we seek to extract the Helmholtz equation with matrix coefficients that is the hybrid transformed version of the required matrix Klein-Gordon equation. That also gives rise to the Schrödinger equation as an approximation.
Our primary wave equation in its hybrid form as EZhybrid above states:
A Minkowski vector divergence operation column by column or row by row respectively can be applied to the auto-spectrum from equation EFspect above and the result is a zero vector where ψT is analytic:
But we can apply both of these operations together and thereby achieve a scalar zero result so long as we allow that the combination of the left and right lozenge operations needs to be corrected on a matrix element by element basis for interaction effects of commutation and multiplication to preserve their respective individual operations. Using this device we may establish as no more than a consequence of the axioms of the model that overall continuity of correlation, expressed here in terms of the auto-spectrum, is maintained according to this particular sort of constraint on divergence.
We shall require Anticommutation of Mixed Partial Differentiations (let us abbreviate this to AMPD here). This is an issue that in the context of the wave equation alone does not arise because it makes no explicit reference to interactions involving orthogonal co-ordinates. However, as soon as correlations or power spectra are considered there are products involved that connect mixed pairs of co-ordinates, and the question of symmetries between the factors involved then brings us face to face with it. Thus, in order to ensure the existence of rotative symmetry in a physical three space (i.e. freedom to arbitrarily relocate our co-ordinate system by rotations) we must prescribe the right structure to support it.
Without this feature in our model the effects of the sense of positive and negative directions of the spatial co-ordinates would remain fixed with the result that any interactions would form a symmetry about the axis along which all three co-ordinates are of equal value. There would thus be a special direction as fundamental in the space. Quite contrary to this we need to model a system that displays the same behaviour regardless of rotations in the basis of spatial co-ordinates. In simple terms, the length and behaviour of a stick must be able to remain constant regardless of the direction in which it points. Thus in the three dimensions of physical space we need Pythagoras theorem to work regardless of choice of rotated co-ordinate systems ... the space must have a Euclidean metric that does not depend on rotative direction. Similarly the properties, such as cross couplings, associated with any successive pair of orthogonal axes (say from x to y) must reverse in sign if the sequence is reversed (from y to x).
To see how this comes about we may consider facing along the x-axis with the z-axis upward; then the y-axis will be positive to our left and negative to out right. If we turn to look along the y-axis then the x-axis will be negative to our left, so a system rotated in that way would change its behaviour if it were determined by absolute co-ordinate values. Instead we need to reverse the sign of any coupling between two axes if we reverse the order in which we involve them. To do this we must first establish a preferred sequence of the axes, such as x, y, z, and that sets up a handedness of positive rotation (a chiral orientation). We may then treat any pair taken in that sequence as positive in effect, and any pair taken opposite to that sequence as negative.
When this is done in choosing the sequence of orthogonal co-ordinate axes for a pair of partial differentiations then this convention will determine whether the result needs a sign reversal or not. With successive partial differentiations on the same axis the issue does not arise ... no sign reversal is ever needed. When laid out as a matrix the pattern of sign reversals forms a chequer board over all of the off-diagonal elements, and with the opposite half matrices having opposite signs (antisymmetric off-diagonal triangles).
We do not need it here for the case of rotations in only three dimensions but subject to some additional permutation rules this type of patterning can be applied in a Euclidean space of any number of dimensions, and it is always concerned just with how any dimensionally mixed pair of operations is handled. In the tensor mathematical terminology the operator generating this sign reversal pattern is referred to as the "Levi-Civita connection" (pronounced Leyvee Chivveeta in Euro-speak).
With the hybrid vectors we use here where frequency replaces time the pattern does not extend directly to the fourth dimension of frequency. In any case that axis relates with geometry that is Minkowskian (hyperbolic) rather than Euclidean (trigonometric). However the antisymmetry is still present, brought about by the squaring of the imaginary factor j. It still finds its way in!
Commutation of differentiators introduces the off diagonal chequer board pattern of sign reversals from the anticommutation effect of mixed partial derivatives (see AMPD above). For the hybrid type of operators these arise in the three space dimensions but not in the frequency dimension because there they operate through simple multiplication that is commutative. However this remaining dimension still involves a sign reversal (Clarify this). Combining these requirements we can build a matrix L defined thus:
|
EmatL |
This matrix can then be applied element by element to the direct (Cartesian) product of a pair of operators to generate a bilinear divergence operator (it contracts a 4×4 square matrix to a scalar). This achieves the application of two divergence operators simultaneously to a spectrum that is itself a bilinear product of two gradients. Thus we need to extend the vector notation to carry two vectors simultaneously as a direct product along with a modifying matrix. This cannot be reduced to successive operations of simple vectors and matrices.
We could resort to tensor notation at this point, but in view of the desirability of using hybrid vectors that would be awkward too. So I shall extend the vector notation a little so as to handle the excursion into the second degree brought by correlations and spectra and the way that then paired vectors operate simultaneously in direct product as matrices.
Operators of this bilinear type must be applied by means of a matrix inner product, shown by symbol  here, to the auto-spectrum matrix to yield a scalar invariance equation. To do this also needs symbols for the operation of direct vector product modified by a matrix, and is shown here in the form of the direct product symbol
here, to the auto-spectrum matrix to yield a scalar invariance equation. To do this also needs symbols for the operation of direct vector product modified by a matrix, and is shown here in the form of the direct product symbol  split to enclose the matrix symbol as in
split to enclose the matrix symbol as in 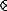 L
L 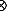
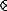 L
L 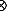 M·◊−jξT]
M·◊−jξT]  ΦTT(jξ, x, t) = 0
ΦTT(jξ, x, t) = 0... where ΦTT is the self spectrum matrix of the total field, containing both substrate and derived parts together.
For general convenience we may allow that any number of matrices may be incorporated into the product as a succession of factors separated by the symbol  so that the extended inner product result is the sum of all of the corresponding element by element products over all of the factor matrices. Where elements are sensitive to commutation (as is the case for differentiator elements) then any commutative manipulation of the factor matrices is only permitted subject to the commutation restrictions of the elements within the respective matrices. Thus the above equation may alternatively be written as:
so that the extended inner product result is the sum of all of the corresponding element by element products over all of the factor matrices. Where elements are sensitive to commutation (as is the case for differentiator elements) then any commutative manipulation of the factor matrices is only permitted subject to the commutation restrictions of the elements within the respective matrices. Thus the above equation may alternatively be written as:
 ◊−jξT]
◊−jξT]  M·L·M
M·L·M  ΦTT(jξ, x, t) = 0
ΦTT(jξ, x, t) = 0... or yet again, since the matrices containing only constants (no differentiations) can commute under the
 operator:
operator: ◊−jξT]
◊−jξT]  ΦTT(jξ, x, t)
ΦTT(jξ, x, t)  M·L·M = 0
M·L·M = 0
Shortcomings of the Symbolism
I am not altogether happy with this extended vector notation. Still it is better than just going to tensor notation being more diagrammatically dramatic with its symbols and more evocative of the structure in the lay concepts of the Minkowski 4-space (i.e. handling a compound 2-vector with an irregular algebra). In this latter respect it makes a positive play of the broken structure of the hybrid vectors and operators.
What seems to be needed is a vector notation slightly extended to encompass rank 2 tensors as direct products of vectors, and in which the contraction operation is symbolised separately instead of being implicit in the application of a differentiator symbol as is the case in conventional vector notation. This would then allow manipulation of the rank 2 tensors before having to contract them into some sort of divergence.
The issue of whether we can continue to use sequence in the line of text to convey structure of operation seems to be critical. Taking a leaf from Feynman's book, perhaps resort to some kind of line and node flow diagram in two dimensions would do the job better.
If I have missed any existing symbolisms which might do this job or if anybody has suggestions in this respect I would be pleased to hear of them with a view to improving the presentation of this essay.
For the sum of our substrate and derived fields ψS and ψD taken together the hybrid wave equation then says:
So we may state an invariance involving separated auto and cross spectral terms making up the total auto-spectrum for frequency ξ thus:
 ◊−jξT]
◊−jξT]  (ΦSS(jξ, x, t) + ΦSD(jξ, x, t) + ΦDS(jξ, x, t) + ΦDD(jξ, x, t))
(ΦSS(jξ, x, t) + ΦSD(jξ, x, t) + ΦDS(jξ, x, t) + ΦDD(jξ, x, t))  M·L·M = 0
M·L·M = 0
We know from symmetries in the definition of the correlation and spectrum functions that
Thus the same kind of time/frequency reversal, transposal, complex conjugation symmetry exists throughout the correlations/spectra.
So we can write a Whole Field Spectral Invariance Equation as:
[◊jξ  ◊−jξT] ◊−jξT]  (ΦSS(jξ, x, t) + ΦK(jξ, x, t) + ΦDD(jξ, x, t)) (ΦSS(jξ, x, t) + ΦK(jξ, x, t) + ΦDD(jξ, x, t))  M·L·M = 0 M·L·M = 0
|
ESspec |
From this equation we will be able to split out the paths to different areas of modelling as follows:
Electrodynamics
For electrodynamics the term ΦDD is treated as having little effect, allowing bilinear factorisation within a Klein-Gordon equation as an approximation. Marginal changes in ΦSS and their coherent coupling via ΦK to matter waves ψD generate the Maxwell wave system. This model loses its usefulness as increasing temperature destroys the duration of persistence of electronic states. The electron rest mass is equivalent to
Chromodynamics
This is similar to electrodynamics but the term ΦDD returns to mediate stability in intense centric processes. The upper limits of temperature for this model are much higher than those for electrodynamics because all the frequencies and hence energies involved are some thousand to ten thousand times greater.
Plasma
Where high temperature destroys the persistence effects of steady state remaining near to attractors it reduces the applicability of the electrodynamics or chromodynamics models so resort to statistical modelling of the resulting highly dynamic system as plasma is then necessary. The correlative and spectral approximation methods based upon short term averages remain applicable for those processes where the rates of change of wave function form (real part of the temporal exponential characteristics) are much less than the wave function frequencies (imaginary parts of the temporal characteristics), but not otherwise.
Cosmology
Variations of intensity in ΦSS, and particularly its progressive transformation to higher frequencies by interactions with matter, produce gravitational accelerations and relative changes in perceived metrical systems and lead to a perception of endemic red shift with distance. These phenomena are significant mainly in the large scales of cosmological structures.
Before taking separate paths of approximation we may analyse the nature of the coupling correlations and spectra.
Substrate Scattering Effects:
Consider the steady attractor wave function for a single mode n being a derived field with discrete frequency of the form:
So the (column vector) gradient for this single mode is:
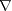 ]Ψn(x) = cis(ωnt).◊jωnΨn(x)
]Ψn(x) = cis(ωnt).◊jωnΨn(x)... Note:
Perhaps it is helpful to see how the correlation generating φSD for the single mode n may be transformed:
 ◊TψD(t + tA + τ, x) dtA
◊TψD(t + tA + τ, x) dtA cis(ωn(t + tA + τ).◊jωnTΨn(x)) dtA
cis(ωn(t + tA + τ).◊jωnTΨn(x)) dtA ◊jωnTΨn(x)
◊jωnTΨn(x)The correlation in the above expression is equivalent to a convolution with the sign of time reversed in one of the two functions. This reversal can be implemented by conjugating the cis factor in ψD. By writing the relationship in the frequency domain the convolution transforms to a multiplication, and the overall multiplying cis factor takes effect as a translation in frequency.
Transforming these time domain expressions into the frequency domain in this way and considering just the steady state for Ψn and statistically also for ΨS (because we can easily put back in the temporal perturbations later when necessary) gives:
 ◊jωnTΨn(x)
◊jωnTΨn(x)So the substrate coupling matrix can be built for the case of a single modal wave as:
 (◊jωnTΨn(x)) + ((◊−jξΨS(−jξ − jωn, x))
(◊jωnTΨn(x)) + ((◊−jξΨS(−jξ − jωn, x))  (◊jωnTΨn*(x)))T
(◊jωnTΨn*(x)))T= (◊jξΨS*(jξ − jωn, x))
 (◊jωnTΨn(x)) + (◊jωnΨ*n(x))
(◊jωnTΨn(x)) + (◊jωnΨ*n(x))  (◊−jξTΨS(−jξ − jωn, x))
(◊−jξTΨS(−jξ − jωn, x))
We may also substitute for this single mode derived field auto-spectrum a spike function
 ◊−jωnTΨn(x)
◊−jωnTΨn(x)Substituting back to expand ESspec we have:
 ◊−jξT]
◊−jξT]  {ΦSS(jξ, x) + δ(ω − ωn)(◊jωnΨn*(x))
{ΦSS(jξ, x) + δ(ω − ωn)(◊jωnΨn*(x))  ◊−jωnTΨn(x)
◊−jωnTΨn(x)+ (◊jξΨS*(jξ − jωn, x))
 ◊jωnTΨn(x) + (◊jωnΨ*n(x))
◊jωnTΨn(x) + (◊jωnΨ*n(x))  ◊−jξTΨS(−jξ − jωn, x)}
◊−jξTΨS(−jξ − jωn, x)}  M·L·M = 0
M·L·M = 0
For the purposes of a wave model of electrodynamics we must derive from this equation two reduced equations. One must be derived by incoherent summation of substrate power and coherent summation of coupling effects to yield a Helmholtz equation in
We can substitute
Making substitutions and expanding builds the Substrate Spectral Divergence Equation thus:
 ◊−jξT ] ◊−jξT ]  ΦSS(jξ, x) ΦSS(jξ, x) | Ediv.0 Substrate divergence |
 ◊−jξT ] ◊−jξT ]  (δ(ξ − ωn).(◊jωnΨn*(x)) (δ(ξ − ωn).(◊jωnΨn*(x))  ◊−jωnTΨn(x)) ◊−jωnTΨn(x)) | Ediv.1 Strong coupling |
 ◊j(−ξ−ωn)T ◊j(−ξ−ωn)T | Ediv.2 Electromag couplings |
 [jωn, 0]T [jωn, 0]T+ [jωn, 0]  ◊j(−ξ−ωn)T ◊j(−ξ−ωn)T | Ediv.3 Charge & current origination |
 [jωn, 0]T ] [jωn, 0]T ]
| Ediv.4 Compton constant |
 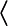 (◊jξΨS*(jξ − jωn, x)) (◊jξΨS*(jξ − jωn, x))  ◊jωnTΨn(x) ◊jωnTΨn(x)+ (◊jωnΨn*(x))  ◊−jξTΨS(−jξ − jωn, x) ◊−jξTΨS(−jξ − jωn, x) } }  M·L·M = 0 M·L·M = 0
|
The divergence balance equation is bilinear in the amplitudes and as such it has things to say about power flow balances. These effects are statistically incoherent. They can lead to gradients of the ambient intensity of the substrate, and thereby to the general relativistic aspects of the model. For the special relativistic cases such gradients are, by definition, negligible.
The equation also produces couplings in the form of coherent scattering of substrate amplitudes due to the presence of the derived field. It is these latter coherent correlative effects in the substrate that bring about the Maxwell wave system. They propagate merely as part of the substrate field, decaying in intensity according to the inverse square law with distance. They are induced by the terms in Ediv.3 that represent charge and current origination. They affect matter via the terms in Ediv.2.
The term Ediv.4 labelled as "Compton constant" is the non-differential term that appears in Klein-Gordon or Schrödinger wave equations and is responsible for defining the Compton frequency, and thereby the electron rest mass.
The term Ediv.1 labelled as "Strong coupling" is the source of the so called "strong force" that appears as part of the conventional description of nuclear processes (chromodynamics). Note that it is of quadratic degree in the intensity of the derived field whereas the electrodynamic effects (Ediv.2, .3 and .4) are all of linear type. To a first approximation is has no effect upon electrodynamics models because their derived fields are much weaker than the substrate.
This equation is a divergence balance that takes a given derived mode wave function ψn with its discrete frequency ωn and applies it to determine statistical differential divergence contributions to the substrate field linking all pairs of substrate frequencies that satisfy
We can take advantage of some approximations as follows:
- Substrate has wide bandwidth - The substrate spectrum is finite but its bandwidth is many decimal orders of magnitude greater than any of the values of derived mode frequencies we shall encounter and the spectrum is smooth so that over intervals equal to derived mode frequencies we are able either to use a first order slope approximation for intensity versus frequency or for some purposes even to neglect the slope altogether.
- Substrate has high intensity - For electrodynamic processes the ratio of derived field intensity to substrate field intensity is very small.
- Substrate is near equilibrium - The substrate spectrum remains very close to being an even function of frequency. It is small coherent deviations from this statistical equilibrium symmetry that convey the Maxwellian radiation, and they are induced by charges and currents. When the effects are integrated across the very wide band of the substrate frequency ξ the statistical fluctuations remaining as effects upon the derived field are very small. (We might query the relationship between the minimum random noise coming from the substrate and the electromagnetic zero point fluctuations caused by the ubiquitous restriction to quantal interactions. Are they just two views of the same thing?)
Rather than attempt to use all of this equation Ediv as a single piece we may benefit by separating approximations that describe sub or factor processes more or less independently. The conventional processes to consider in this way are electromagnetics, electrodynamics, chromodynamics (i.e. nuclear) and gravity (i.e. general relativity). These respective sub-models can be extracted from the Ediv equation by interpreting its terms as follows.
 ◊−jξT ] ◊−jξT ]  ΦSS(jξ, x) ΦSS(jξ, x)  M·L·M M·L·M | Ediv.0 Substrate divergence |
This is the energy divergence of the substrate wave which must remain at zero in free space propagation (i.e. where there are no modal/derived/matter waves).
 ◊−jξT ] ◊−jξT ]  (δ(ξ − ωn).(◊jωnΨn*(x)) (δ(ξ − ωn).(◊jωnΨn*(x))  ◊−jωnTΨn(x)) ◊−jωnTΨn(x))  M·L·M M·L·M | Ediv.1 Strong coupling |
This term balances with the substrate intensity in nuclear processes. Because it is quadratic in the modal amplitude and the fact that electronic fields are much less intense than the substrate, this term is very small in electrodynamics modelling.
 ◊j(−ξ−ωn)T ] ◊j(−ξ−ωn)T ]  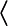 (◊jξΨS*(jξ − jωn, x)) (◊jξΨS*(jξ − jωn, x))  ◊jωnTΨn(x) ◊jωnTΨn(x)+ (◊jωnΨn*(x))  ◊−jξTΨS(−jξ − jωn, x) ◊−jξTΨS(−jξ − jωn, x)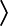  M·L·M M·L·M | Ediv.2 Electromag couplings |
Coherent correlations in the substrate field act to generate reactive (imaginary) biases to the coefficients of the equation determining the modal resonance mechanism. The biases can be summarised in the coupling matrix generating the differential operator of the modal Klein-Gordon wave equation.
 [jωn, 0]T + [jωn, 0] [jωn, 0]T + [jωn, 0]  ◊j(−ξ−ωn)T ] ◊j(−ξ−ωn)T ] 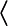 (◊jξΨS*(jξ − jωn, x)) (◊jξΨS*(jξ − jωn, x))  ◊jωnTΨn(x) ◊jωnTΨn(x)+ (◊jωnΨn*(x))  ◊−jξTΨS(−jξ − jωn, x) ◊−jξTΨS(−jξ − jωn, x)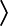  M·L·M M·L·M | Ediv.3 Charge & current origination |
The four vector gradient of the modal wave acts to induce coherent patterns of divergence in the substrate with no more influence on the modal wave than a noise fluctuation. These inductions in the substrate field can be summarised as the charge and current originations driving the Maxwell field of electromagnetic radiation, and the form of that induction is expressed in equation Echarge.
The induction when expressed in terms of the time domain (as opposed to the more usual frequency domain in these essays) involves the appearance of a Hilbert transform in the formula. That occurs as a result of the phase relationships inherently present in this wave process ... see equation EHt. An explanation of this otherwise tricky notion needs to be expanded here.
 [jωn, 0]T ] [jωn, 0]T ]  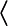 (◊jξΨS*(jξ − jωn, x)) (◊jξΨS*(jξ − jωn, x))  ◊jωnTΨn(x) ◊jωnTΨn(x)+ (◊jωnΨn*(x))  ◊−jξTΨS(−jξ − jωn, x) ◊−jξTΨS(−jξ − jωn, x)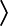  M·L·M M·L·M | Ediv.4 Compton constant |
This is the term that allows the intensity of the substrate wave to provide support for existence of a derived wave (a modal wave) with its group velocity below the speed of light. By integrating across the bandwidth of the substrate this term allows the dispersive loading term in the Klein-Gordon equation for electrodynamics to be obtained from the mean energy density of the substrate.
 Electromagnetics
Electromagnetics
For free space we may omit all derived field terms from Ediv leaving just the Ediv.0 term. This leads to the Maxwell system of wave propagation for free space. For the substrate field alone, in the absence of the derived field corresponding to matter, the self spectrum matrix Φ00 of the pure native wave field must satisfy:
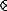 M·L·M
M·L·M 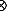 ◊−jξT]
◊−jξT]  Φ00(jξ, x, t) = 0
Φ00(jξ, x, t) = 0The dynamic correlations of the substrate field can be interpreted as the basis of the electromagnetic field.
The interaction effects carried by modulations of the substrate field are in a general sense extremely complex. A first approach to bringing some simplification to this situation as an approximation is to study the 4×4 substrate correlation matrix φSS of which the sixteen elements are temporal correlation functions between pairs of the four substrate field derivatives, as discussed here above. That reduces the task to studying the interaction dynamics in terms of the statistical correlation parameters rather than the underlying wave variable itself. However we need to go further than that.
Reciprocal Moments of Correlation Functions:
So long as the bandwidth of the substrate field is much greater than the modal frequencies of any derived field (matter waves) then a good approximation of these interactions can be constructed in terms of the first reciprocal moments of these same correlation functions that link pairs of the four partial derivatives. The reciprocal relationship arises because the spectral shifting effect induced into the substrate field by scattering from a derived wave mode with a given amplitude is proportional to the frequency of that mode. It is only this induced spectral shift that carries the causal effect of this interaction; the specific value of modal frequency inducing it does not otherwise matter. This is a result of the reliable degree to which the substrate noise is incoherent with any modal motion we may consider.
Here we may see that the first degree in frequency that multiplies this interaction produces the nature of charge, whilst the concept of energy involves a multiplier in the second dgree of the modal frequency. The ratio of the two carries the Planck proportionality between energy and frequency for a given charge.
The above approximation for substrate induction is made particularly powerful in the electrodynamics case because then it involves only very small perturbations about a statistically isotropic and equilibrated form of the substrate correlations. This approximation corresponds to the electromagnetic field as it is conventionally considered. In terms of the 4×4 substrate correlation matrix φSS on time delay τ the approximation can be built as 4×4 matrix
| θ(t, x) = | ∞ | (φSS(τ x, t)/τ) dτ | |
| −∞ |
The same result can alternatively be built from the equivalent frequency domain spectral matrix ΦSS on frequency ξ as:
|
The variable t is left present to accommodate the relatively slow variations of these statistical parameters in a slowly perturbed steady state approximation form of model. It is reintroduced as the first element of the argument in
These expressions amount to pre-integrating the coupling effects across the substrate spectrum before applying them to any or every derived wave component, each with its particular value of frequency. To do this they rely upon a certain amount and type of smoothness of the substrate spectrum ... a moderately good approach to its statistical equilibrium form. Such is the aggregated nature of the substrate spectral influences summarised in the Maxwell field. The resulting variable θ is a 4×4 matrix of imaginary scalars corresponding to the elements of the electromagnetic field vectors and composed as follows:
|
... where [u1, u2, u3] is the electric field vector and [v1, v2, v3] = [θ23, θ31, θ12] / j is the curl of what is conventionally called the magnetic vector potential. Seen in terms of this way of modelling the term "vector potential" is an unsuitable name left over from the Lagrangian way of looking at things so does not really fit in here, but we still use it. Each element of the matrix
The diagonal elements of this matrix are inherently zero due to the way it is derived from the correlation matrix. The diagonal correlation elements are autocorrelations and are therfore real even functions, and they produce a zero result under the operation of reciprocal moment evaluation.
To handle the presence of matter the charge and current source terms from Ediv.3 can also be added, but in ordinary electromagnetics these are usually expressed explicitly rather than as obtained from the distributed form of the modal wave functions. So expressed in this more comprehensive form it will look more complicated if the detail is expressed. Unless spin based effects are at stake, such as in the Aharonov-Bohm effect, there is little reason to go to that extra trouble.
 Electrodynamics
Electrodynamics
For the purposes of electrodynamics the term in Ediv.1 is negligible at least for a first approximation. The term depicted in Ediv.3 is balanced by adjacent pairs with respect to couplings between the substrate and derived fields whereas those in Ediv.2 and Ediv.4 are not. This .3 term has effect upon the substrate in coherent and therefore strong ways involving oppositely signed frequencies. By contrast its effect on the derived field, because of the balance, is of zero mean and incoherent across the substrate frequencies. Thus it has no more effect upon the derived field than to create a fine high frequency fluctuation about its steady value with no net mean effect. Integrations are required here to show this point clearly and rigorously.
So, neglecting a wide band noise term, the immediate effects upon the derived field can omit the .3 term leaving the overall process to bring the influences back via the .2 term after propagation in the substrate. There are however divergence terms, both electric div and magnetic div curl, buried in the structure of the .2 term, and these will take effect upon the derived field without any propagation delay at all. These provide the causal basis for spontaneous quantisation ... see Smooth and Quantal Properties of the Complex Wave.
Using these ideas we can separate the charge/current part of the model from the electron wave dynamics part in building the overall causal electrodynamics model. I shall show here how this generates the coefficient matrix for the Klein-Gordon wave equation.
Couplings to Matter:
The electromagnetic field elements of the matrix θ can be applied to express couplings between derivatives of the derived wave that depend upon the substrate spectral form. They enter as the off diagonal elements of the matrix defining the 2-form of the differential operator for the derived wave constitutive equation. However, if we wish to work with the hybrid form of vector expressions then the electric field terms in the leading row and column must have the frequency of the respective mode to which they are being applied divided out. This is because ...
 Scaling the Fields
Scaling the Fields
The system defined in terms of the native substrate field plus the derived field solitonic components is based upon coordinates with no particular definition of scale because it is on a projective space, which means that proportionality is all that is inherent. The only source of scale in such a model arises from the bandwidth (a time/space gauge) and intensity (an energy density gauge) of the ambient substrate field. Thus in our model here it is natural to normalise the scales in any region of space in some way based upon these two attributes of the substrate. This can in fact be done, but for the purposes of establishing length and energy scales in electrodynamics the two constants are best involved in a somewhat indirect way that will now be described.
It must be remembered that isotropy and uniformity of the substrate are not inherent. This is unlikely to be of great importance except in large structures (cosmology) where a general relativity is needed or in intensely excited matter (nuclear plasma) which is another more general area of stochastic analysis altogether!
Notice that thinking of general relativity in this way suggests variable scale gauge factors over a special relativistic uniform (flat) coordinate system as opposed to the more conventional scheme of curved space with fixed scale gauge factors. These reciprocally conceived schemes of general relativistic modelling can be made equivalent at least for approximations under moderate degrees of gauge variation without singularities. Nevertheless the two schemes cannot ever be completely equivalent because the substrate field establishes two scale parameters whilst the conventional general relativity normalises only one. In its raw form this extra parameter sets the very small constant that in the Standard Model of conventional physics is referred to as the Planck time/length.
Rather than using the Planck time as a basic scale in electrodynamics it is more attractive to use the Compton frequency. From ???? this can also be seen to be dependent upon that very small time but in combination with the other scale constant for the energy density.
 Nuclear Dynamics
Nuclear Dynamics
The quadratic dependence in Ediv.1 upon the derived field allows this term to compete with and thereby locally to attenuate the intensity of the substrate field in those regions where the derived field reaches very high intensities. Such is the basis for nuclear, and particularly quark, structures. Suitable approximation to convey the nature and stability of such structures will be left for development elsewhere.
 Gravity
Gravity
There are parts of the wave process that lead to bandwidth broadening and the consequent increase of entropy of the substrate field. This occurs in some very weak degree associated with the modulation of the substrate by matter through its actions in the Ediv.3 term. However, there is also an effect of "tearing apart the fabric of the wave" that must occur in a small measure close to every spin axis. Apart from the super plasma situations that might occur in a star it is probably the latter that contributes most of the spectral up conversion producing the ordinary gravitational and apparent red-shift effects we encounter. This is a big subject and is left for development elsewhere.
 Conclusions
Conclusions
A wave mechanics in which an energetic substrate field drives local interactions and that carries the symptoms of those interactions into the distance at the speed of light with decreasing strength (and is even symmetrical in it effects with reversal of time) appears very suitable as a basis for the under layer of physics. To develop this into the areas of temporal irreversibility and the structure of observation refer to Essential Structure in Physical Observation and Smooth and Quantal Properties of the Complex Wave.
Until further checks are completed it remains unclear whether this model will be truly compatible with conventional quantum mechanics and the "Standard Model" of nuclear particles. However, it is already clear that it has value as a means of comprehension, and brings into cohesion a variety of concepts that have traditionally appeared as arbitrary and disjoint. The prospect for accounting for the superficial aspect of the appearance of particles looks to be a routine matter, dealing with such as Compton effect, cloud and bubble chamber tracks, Stern-Gerlach phenomena, photoelectric effect etc. Similarly the otherwise anomalous effects of apparently non-local deviations of correlation in particle detection can be submitted to a new view in which there appears every possibility that the results will stay within the range of phenomena attributable to causal wave phenomena. All of this work is, on my part so far, in a state of patchwork draft.
 Appendices
Appendices
 A: Elements of an Emergent Non-linearity
A: Elements of an Emergent Non-linearity
Non-linearity emerges from the linear Minkowski wave equation model. One might wonder just what we mean by "linear". It can either be the restriction of the model equations to zero and first degree terms or it can mean the conformance of system behaviour to the superposition principle. To my continuing surprise these appear to be subtly but importantly different.
As a good starting model to see this it might be useful to think of a linear 3D + time Maxwellian model bounded by reflective walls. With fixed walls it is a linear system, but if you allow the walls to move in response to the radiation pressure or some such function of the wave amplitude, then the system becomes non-linear. Now in allowing the walls to be movable in that way you can see how we have let the non-linearity into the model. If we now use a Minkowski geometry and just use a complex scalar wave equation then we can show that reflective entities (field singularity centres of spin) can be realised within the wave system as nothing more than wave structures of the same sort. These act like boundaries, except that they are at points within an otherwise unbounded physical space of the wave functions. So because the resulting structures (that are what we refer to as "matter") can change shape under influence of the field, non-linearity has then been introduced, but without anything more than the same fabric as the wave function itself!
So the system behavioural non-linearity can arise in a system modelled by linear equations. It took nothing more than Minkowski geometry (relativity) and a particular kind of singularity to make that happen. We need a grasp of that singularity and its associated fields.
Two concepts of linearity: formal (zero and first degree) and observational (observed superposition).
The role of singularity (necessary for spin and thereby isolated eigenmodes and persistence of substance).
Observation is essentially based on 3D existence (persistent substance).
The relativistic distinction makes the difference - we live in a projection.
 B: Commutativity and Conformality
B: Commutativity and Conformality
To enable certain deductive reasoning we are concerned to clarify where we have well behaved nature that we may call smoothness and analyticity of the wave functions in our model. We have to deal with the occurrence of deviation from analytic nature in the form of line singularities. The notions of Cauchy-Riemann differentiability in the plane and its possible or necessary existence in certain planes within the Minkowski 3+1 dimensional geometric space will be significant.
Scalars, real or imaginary etc., are commutative in multiplication, namely
We may seek further entities that under multiplication produce a product in the same domain (so inner and direct products of vectors are excluded) and that are commutative. The question can be applied in the domain of square matrices of scalar elements under the usual column and row rules for multiplication. Thus we may recognise the possibility that a given pair of such elements may be either commutative or not.
Breaking apart these matrices we may see that the condition for commutativity is that the inner product between rows j of one element and columns k of the other shall obey the rule
We may apply a matrix coefficient to a pair of first order vector differential operators to produce a quadratic form. We build our model from this type of compounded differential operator in which the matrix is permitted only to be Hermitian.
Non-commutative nature only appears when we do things that make the imaginary parts of the transformation matrices give rise to observable effects and that can only be in connection with processes involving the second differential order, and therefore in a general sense is not so readily evident.
Show that functions satisfying the MKG equation have at every analytic point a direction of amplitude gradient, and that the conjugate planes to these form closed surfaces, the two together forming a conformal system.
 References and Background Reading
References and Background Reading
This symbol denotes linkage to an independent web site: ![]()
| [ABoES] | A.G.Booth "Essential Structure in Physical Observation" http://wavemodel.org/obs/observ.html |
| [ABoSQ] | A.G.Booth "Smooth and Quantal Properties of the Complex Wave" http://wavemodel.org/qed/smooth.html |
| [ABoWT] | A.G.Booth "Wave Topology of a Spin Mode" http://wavemodel.org/spin/spin.html |
| [ACo05] |
A.J.Coleman "Whitehead's Principle of Relativity - Unpublished Lectures by J. L. Synge, FRS" Queen's University, Kingston Ontario May 2005 |
| Phone and e-mail see foot of Wavemodel home page. | ||
| Copyright © A.G.Booth 2005 All rights reserved | ||