|
Smooth and Quantal Properties of the Complex Wave |
| A.G.Booth | WWW original 8 April 2004 | Copyright © A.G.Booth, London 2004-2005 All rights reserved | ||
| Document ident: | Last updated 25cMarch 2006 | Smooth and Quantal Properties of the Complex Wave. A.G.Booth | ||
Keys: |
quantize quantized quantization |
|||
This document makes use of the HTML character entities in its text, so if your browser does not support them you will see the raw HTML tags that call them up. Preferred browser is Firefox, but I believe that the text should display adequately for versions starting from v4.5 for Internet Explorer, v6 for Netscape and v6 for Opera.
 Contents
Contents
- Summary
- Introduction and Motivation
- Electronic Interactions
- The Causally Completed Model
- Charge and Magnet Origination
- Charge Quantisation
- Fine Structure Constant
- Discussion
- Appendices
- A: Statistics and the Lagrangian Model
- B: Three Wave Couplings
- C: Charge, Current and Physical Phenomena
-
D: Coupling Field Integrations
- E: Temporal Smoothing of Charge
- F: Mathematical Groups and the Pure Wave Model
- Acknowledgements -->
- References and Background Reading
 Summary
Summary
Complex scalar waves in continuous space are capable of displaying a special kind of smoothness of dynamic properties, and this feature applies in particularly interesting ways to the Minkowski relativistic sorts of
The conventional approach to physics based upon primacy of the Lagrangian model of dynamics obscures this characteristic smoothness and consequently leaves an impression that the ultraviolet catastrophe is bound to occur. Having started with such "noisy" models this impression is then very hard to dispel by reasoning, a problem that is rampant in late twentieth century quantum electrodynamics. In contrast we pursue here an Eulerian model of continuous complex fields until, in the simplest sufficient form compatible with observed reality, it reveals the emergence of quantal phenomena in its behaviour.
The objective here is to explore and develop the especially smooth nature of interactions in the class of complex waves in a continuum so that models may be created that do not start with the disadvantage of implausibility at high frequencies. Where such models are applicable, and that appears to be the case in the complex variable wave dynamics of sub-quantal physical processes, the resulting approach is often simpler both to understand and to manipulate than are models based on Lagrangian ideas.
 Introduction and Motivation
Introduction and Motivation
A wish to find better working models in electrodynamics motivates this work. There are problems with the basic paradigm of twentieth century physics, in which a deterministic wave process provides the wave function from which is derived the probabilities of the state in which "each particle may be found". An implicit abandonment of the principle of causality in such a model leads to difficulties in physics where it shows up as observable phenomena demanding the status of non-local causation. Also in applications such as engineering the departure from underlying rigorous causal logic impedes comprehension and development by the individual non-specialist worker.
Here we study a model that is deterministic and continuous throughout, and in which the essentials of uncertainty and quantal phenomena arise as emergent in the inherent and unavoidable characteristics of the processes of observation by an observer who is also part of the wave continuum. This is done at least in the hope of providing some useful approximate models that are more logically tractable than usual physics theory, and of exploring to expose and extend the limits of development of continuum wave models of this sort.
We might think of the microscopic processes as involving particles because we seem always to see them in the detection process. More strictly we see quanta, but the immediate conviction still remains that way regarding particles. But if you recognise that there would be no detection possible if it were not for the lumps and jumps nature in the observation process itself, then it comes as natural enough to attempt to describe the whole process on the basis of continuous waves. This is especially true if the resulting model can account for the complete results, including the means to quantisation, because it is evident that the particle based models cannot do so without at least some seriously counter-intuitive parts being added into the model.
Thinking in wave terms the appearance of quantal and particulate results is then to be seen as the consequences of the operation of a wave process under the conditions necessary for observation to be possible. How such quantal phenomena and states can arise in a purely wave based process is then of particularly great interest. In contrast to the idea of the collapse of a probability wave function as per the Copenhagen interpretation of quantum mechanics, in a wave model the detection is not even expected to occur at an instant but rather as the final outcome of a noisy trajectory of state with form that we can infer by the statistical effects but can never observe in specific instances except through its outcome. This is because our observation faculty is itself made of the same kind of processes. It is only after a wave process has settled out into a distinct and durable state that we can consider ourselves as having obtained a result. Significant delay, though it may superficially seem short, is always involved in determining that outcome.
The quantal nature that is the necessary outcome of observation leads us to try to explain the entire process in terms of these discrete outcomes, and that makes us consign the unknowable part of the process leading to each observation to a probability domain. Thus the conventional quantum theory and the Standard Model of particulate quantum mechanics is based upon a deterministic wave process of state evolution followed by a sudden resolution into a discrete state at the point where observation occurs. It leads people to puzzle deeply over how such a sudden event can occur in the observation process, and to wonder if there is any sense in considering the state of something that is not observed (Schrödinger's cat). It even leads to questions of whether there has to be an observing mind involved in order for the probability collapse to occur (Wigner).
These metaphysical questions are OK for debate, but by using a model in which the wave and quantal involvement of interactions in the process of observation are taken into account, no such questions arise. No probabilistic part is necessary in the primary model. Probability is then consigned to handling only the state of things that as finite participators in such a system we do not, and especially that we cannot, know.
This approach does not set out to be different in its predictions about phenomena. It is merely an alternative model in which the convenience of use is improved by greater intuitive value regarding matters of causality. It will, however, require that the user of such a model remove the idea of "particle" from its primal position and replace it with something like "wave" or "field". The photon, though having quantal energy, will be never more than an illusion created by the process of observation. The electron will have no more than partial status as "substance", taking approximately stable form only when it is part of an atomic, molecular or crystalline structure, and behaving as no more than a special kind of waves when in free flight. The nuclear particles such as baryons and hadrons will be regarded as having substantial form as solitons, but will not be dealt with in this essay beyond providing point nuclear charges upon which electronic fields may be centred.
The basis of analysing atomic electrodynamics is developed using a Klein-Gordon like equation to the point where the spontaneous emergence of charge and magnet quantisation is made evident. The use of a Hilbert transform in deriving the charge and current origination from the
So we set out by describing matter as De Broglie's waves in a non-Lagrangian locally causal continuous complex scalar wave model. Within this model interactions, occurring via Maxwell electromagnetic waves, are described in terms of functions of the De Broglie wave state and its derivatives. This is done on a basis that uses no real frame of reference in the complex plane. In other words only relative values of the complex argument (phase) are involved in bringing about these interactions. Such "relativity of phase" is important, and although easy enough to realise in a complex wave model such as when using the Hilbert transform, it presents great difficulties with concepts of either the Lagrangian or particle based sorts. These problems are currently handled by means of gauge theories, whereas no such construct is necessary in the approach taken here. From this model with its built-in Minkowski geometry all the necessary effects are shown to emerge that produce the non-linearity essential to give rise to spontaneous quantisation of electronic fields.
Triplet interactions of wave modes, usually between two resonant complex matter waves and one electromagnetic wave either resonant or propagating ... see Allen and Eberly [AE87], also form an important concept and this is developed in Appendix B.
For an introduction to some basic ideas about observation that offer a platform for this approach to modelling see the accompanying paper "Essential Structure in Physical Observation" [ABoES].
For those who have a conventional background in physics based upon use of the Lagrangian model there is further discussion in Appendix A of why its use is rejected here.
Apart from the nature of Cauchy-Riemann differentiability I have not yet found out and would like to know if and how the mathematical fraternity refer to this "smooth" nature that is peculiar to these sorts of complex waves. They are characteristically smoothly rotative in the complex plane (N.B. that does not mean they necessarily rotate in space) with more or less uniform magnitude whereas real waves must oscillate in their real scalar dimension with repeated transitions through zero. The difference from dynamic systems described by real variables is for this reason dramatic.
 Electronic Interactions
Electronic Interactions
By way of our experiences of basic physical interactions at the atomic level we are most aware of the atomic spectral interactions with an electromagnetic field. Each such interaction usually involves a Maxwellian radiation field and the simultaneous perturbation of the excitation of two atomic electron modes ... see [AE87]. This is the simple case, and the two electronic modes can alternatively be associated with larger structures such as molecules or crystals. The process remains the same in that each interaction involves three elemental field structures, two of them De Broglie matter waves and the other an electromagnetic wave. We can, if we choose, complete the model of interaction by terminating the electromagnetic wave at its "other end" in some other nearby resonant structure of matter. Although this extends the range of dynamics possibilities the elements of the process remain similar.
Viewed in the above way the model of an atom may be seen as continuous in its space of possible electronic excitations, but discrete only in its state of charge quantisation ... say for instance its state of ionic charge. By inducing shifts of the excitation state progressively away from equilibrium an otherwise stable atom can be made to increase its tendency to break from its existing ionic state and change to another. This model accords with quite usual sorts of systems models with continuous state and discrete attractor points near to which the system fluctuates and between which it sometimes jumps. The attractors are associated with the charge structure state, and not with any other aspect of the atom. The excitation levels of the individual electron modes in such a model tend to their Fermi distribution levels (ref here) only as the result of electromagnetic interactions in a thermal milieu. If that thermal interaction is strong then following a disturbance they will return quickly, and if not so strong, then slower. They will always suffer some degree of thermal perturbation about their respective Fermi levels.
It is a widespread usage to consider these states of excitation in atoms to take only quantal values, but in fact there is no direct evidence of this since the only ways in which the quantisation can be observed is by means of the rather more explicit quantal changes of charge state within the processes that are essential to the structure of the observation apparatus ... see [ABoES]. The rules that dictate the relationships of these quantal effects are strict but have a form that allows us to remove them from the electron mode excitations without altering the extent of and limitation to prediction of behaviour of the system. That is what I shall do here. This possibility is rather widely believed not to be true, but that is the result of other assumptions about the possibility of objective observation, and I shall not make those assumptions here. For many purposes this can actually simplify our model and is at least an interesting alternative to the so called "Standard Model" and the non-local "Copenhagen interpretation" that are current in quantum mechanics.
To see that the Fermi distribution comes about, and with it the related Planck distribution of mean energy levels as associated with their respective electromagnetic frequencies, we need only to recognise that non-linear interactions between three lossless complex wave systems at different frequencies produce signed power transfers into the respective systems that are proportional to the respective frequencies and depend upon the phase relationships (see Appendix B). That causes the De Broglie standing mode excitation levels to conform to Fermi-Dirac statistics and produce the Fermi distribution whilst the Maxwellian processes that mediate the energy interchanges follow Bose-Einstein statistics producing spectra that correspond to the Planck distribution of radiation intensity versus frequency.
Herein lies a further heretical point of this model. This is that the principle of power proportional to frequency in interactions applies in terms of "signed" frequencies ... we shall not be free to associate negative frequencies with anti-matter in this model, but fortunately that is not a fatal problem. It does mean that we cannot use the usual ideas surrounding the Schrödinger and Dirac equation models as basic in this respect, but that difficulty will be solved by means of what is in fact a simplification and generalisation in our choice of equation form. The conventional equations remain as approximations which are sometimes useful.
 The Causally Completed Model
The Causally Completed Model
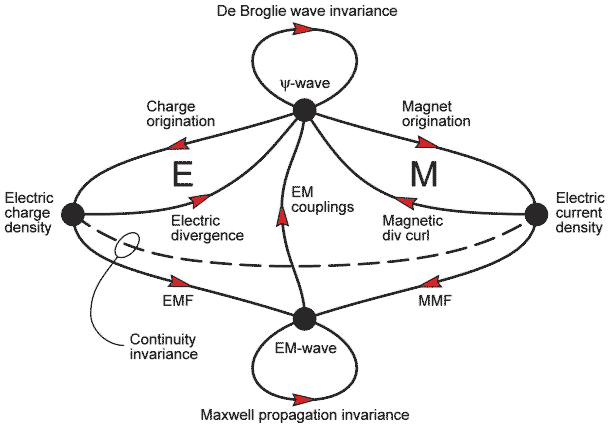
In order to have a closed loop of effects constituting a causal model for electrodynamics we need to depict the origination of charge and magnetic field. This will complete a cycle of causal influences whereby the Klein-Gordon equation mediates the form of electron wave in a given coupling field and the model of charge origination developed here below operating through Maxwellian propagation mediates the form of coupling field for the given electron wave and atomic nuclei. The causal cycle is thereby closed.
|
Each nodal dot represents a variable that has a value at every point in the four dimensional space-time. The
The four-space in which all these fields exist as wave functions is referred to as the Minkowski space to denote the way that one dimension, that associated with time, is treated differently from the other three "physical" space dimensions with their Euclidean geometric properties. This is the basis of special relativity in the model.
The inner loops marked E and M deal with the dynamics of charge and current regulation. Indeed, it is only the E loop that takes effect in determining the distinctions between the discrete attractor states of different ionic charge distributions. Magnetic quantisation involving loop M is more subtle. The remaining causal paths at the lower part of the diagram are via Maxwellian fields. These latter effects are mainly observable as interactions between separate charge or current bearing entities. The processes supporting inter-atomic molecular bonding lie in the hinterland where either or both of these sorts of causal systems may be involved, the upper loops dominating in what are called valence bonds and the lower loops in ionic bonds.
Forces of attraction and repulsion between otherwise intact substantial entities can arise with both sorts of interactions, but the steeply rising potential fields of repulsion (i.e. steeper than inverse square law with distance) typical of the van der Waals forces for close proximity must involve the upper loops in the diagram.
What we know as "force" is manifested in this model by the way that the overlapping of one intact substantial entity by the fields of another inherently introduces an acceleration of its wave structure that can only be nullified by the introduction of some other such overlapping field from yet another substantial entity. It is the systematic quantification of the means for creating and maintaining these field overlaps that we refer to as "force". These acceleration inducing, or momentum transferring, or, as we would account for them in this model, field deforming influences are mutual in certain effects between any two substantial entities, and fortunately these effects can be quantified consistently and abstractly, but nevertheless simply, by vector addition in physical space (Newton's laws). However, it is only in respect of the interactions of supposedly otherwise intact separate entities that the concept can be given a reality. In this model the moving waves are the reality and although lumpy, they are all of a piece and move under local causal field rules. The forces are an abstraction only relevant to an observer that is itself a self identifying part of the system of waves ... you may hypothesise or postulate something or other involving forces, but with this sort of model you do not need to, and indeed cannot, observe (in the explicit sense of "measure") from outside of the system any forces, because there are none described by the model. It is basically a kinematic model.
Thus we have here a type of abstraction that, in spite of having its own sense of absoluteness, is the opposite of the notion in the direct sense of an "objective" model. In this model it becomes clear that we could never in practice be privy to the entire picture simply because we always have to be part of it. The uncertainties in processes of both the quantal and thermodynamic sorts, both of which are fundamental to the processes of observation ... see [ABoES], arise from this nature.
By reference to this sort of diagram we may distinguish two meanings to the word "coherence". The first, which I like to refer to as "quantal coherence", is the locking together into a substantial and persisting whole of a system of wave modes by virtue of their interwoven and shared charge distribution structure. Such is the nature of physical solidity, and physicists refer to such a state as "condensed matter". This is not the normal usage of the word "coherence" in physics, but may well suit the general conception of its lay meaning. After all, at root to cohere means to "stick together". The second, we could call it "wave coherence" and it is the more common meaning in physics, is the sense in which waves of either the De Broglie or the Maxwell sorts may form concentrations in bands of frequency sufficiently narrow that they do not change in relative phase by more than about a radian throughout the space and time of some sympathetic process of interaction. They can then produce exaggerated effects, called interference, through "square of sum of amplitudes" as compared to the smaller "sum of squares of amplitudes" which is all that can be effective in processes where the phases are randomised or chaotic. Seen on this basis the modal waves underlying the quantal coherence of a solid have to be wave-coherent within each mode, but are not so between the modes.
The details of this model must now be painted in.
 Charge and Magnet Origination
Charge and Magnet Origination
To make our closed causal model possible we must define how electric charge and current are manifested in terms of the De Broglie matter wave field. The coefficients of the Klein-Gordon equation are influenced by the distributed form of the charge, and are therefore functions of space-time co-ordinates. Thus we might refer to this form of the equation as a Modulated Klein-Gordon equation, shortened here to MKG. In different forms of approximation the modulated coefficients may be introduced either in the matrix of coefficients of the second differential terms or in the non-differential term in the equation, as discussed below. Such "modulated" forms of the equation are sometimes referred to elsewhere as "Non-linear Klein-Gordon equations", but they are in fact linear so long as the modulated coefficients can be taken as independent of the wave variable. As they are used here below that is a valuable approximation.
This is not the approach taken in conventional quantum mechanics. There the loop of causality is broken by insisting upon quantal values for many of the variables, and where any discrepancies occur the associated integrals are simply normalised to bring their overall value into line with the observed probabilities of quantal detection in experiment. Since a major objective here is to demonstrate the emergence of quantal phenomena such imposition of quantisation would defeat our purpose.
If a useful model of quantisation process can be achieved as set out below then any discrepancy from experiment can still be dealt with by the use of normalising constants at that stage, and to the extent that this is done leaving the model "qualitative only", which would be the same, in this respect, as the conventional quantum mechanics. Application of the model to many things like calculation of the fine structure constant and the Lamb shift provides the tests of this sort.
Physics and engineering concepts of electric potential often appear different, one being absolute and the other relative. In its effects within an atom as described by Schrödinger and Dirac equations, electric potential acts as though it is an absolute quantity whereas in relation to phenomena at greater distances it is manifested as being relative ... a difference between different points in space (consider the enormous potential differences of megavolts involved in a thunder storm that have no absolute effects upon local chemistry).
"Potential" is a concept applicable only in system states with zero relative velocities. Such invariance of integral over different paths cannot be applied generally in the Minkowski 4-space. Therefore it is not suitable as part of a relativistic dynamics model.
Here we deal with these coupling effects only via the Maxwellian field strengths and their rates of change. These involve only local potential gradients and not absolute potentials. To do this the couplings are all introduced into the constitutive Klein-Gordon equation via its differential terms, and in particular its mixed space/space and space/time terms. The Schrödinger and Dirac equations are approximations to this model in which these gradients are pre-integrated to give potentials before installing them in the constant term in the differential operator of the equation. Under those approximations the only possible form of motion consists of steady oscillations (i.e. having zero real part to their exponential characteristic) and at zero group velocity.
We may first describe the way that the electric and magnetic effects (charge and current) arise from the
To comply with the Planck constant proportionality between (modulus of) frequency and observed energy we need a simple model whereby charge will be generated locally as dependent upon intensity (i.e. squared modulus) of ψ excitation in proportion to both this intensity and to its (modulus of) frequency. The following model does this and also suggests a form whereby the field can give rise to a magnetising vector in a related manner. The resulting electromagnetic field can then return as a causal term in the mixed time-space coupling terms in the Klein-Gordon differential operator matrix. It introduces a fixed linkage (that is chirally handed) between sequence of complex value of ψ and handedness of rotation of any directionally oriented form of motion.
A natural first attempt at associating spatial energy density with the ψ function might be simply to use the squared magnitude of the function. However this leads to reduced convenience in the extension of the model to explain coupling effects as will be developed elsewhere. Instead the system is normalised such that the spatial density of energy is associated with the squared magnitude of the time derivative, which is equivalent in frequency domain terms to the squared magnitude of the function multiplied by the square of the frequency. Because of the curious absence of direct coupling between the separate frequency spectral parts of the
The star symbol as in x* denotes complex conjugation.
The copyright symbol used as a binary operator as in A©B denotes the convolution operation (not yet used herein).
Matrices and vectors are set in bold sans-serif type ... scalars: x, X, ξ, Ψ vectors/matrices: x, X, ξ, Ψ.
Symbol T as in XT denotes vector or matrix transpose. An untransposed vector is a column, though
may have its elements depicted horizontally in the line of text.
The dagger symbol as in X† denotes adjugate matrix, i.e. the matrix of signed minors (not yet used herein).
Taking Ht( . ) to denote a time domain Hilbert transform (
| EHt |
Use of a Hilbert transform in the time domain (a non-causal operator that is equivalent to advancing the phase by
So although a non-causal operator (i.e. one having output dependent upon future input) is used, it occurs only in combinations in which the overall effect is causal ... it is no more than a local mathematical construct. An alternative "all causal" model could be built using an explicit pair of real variables throughout in place of the parts of the complex variable, and prescribing the causal relationships using, where necessary, either of the two reals. Use of the Hilbert transform with the complex variable can be regarded as just a shorthand way of doing the same thing.
The phase shifts in the Hilbert and differentiation operations are both
In fact we can go farther over this issue of keeping the causality local. The bilinear Hilbert/integration operation is instantaneous in so far as it can be for any particular temporal wave frequency. Whereas either the integration or the Hilbert transform alone involves temporal non-locality (i.e. memory or prediction), the two together do not. This, in spite of being unworldly, makes it seem curiously more tractable even though we are not used to it in macroscopic physics. It is made possible by the polyphase nature of an "actual" complex variable. It brings about the uncoupling of conjugate wave motions (i.e. those having oppositely signed frequencies). Coupling between electronic waves is then related to algebraic difference of signed frequencies, not the difference of absolute frequencies as must be the case for a system of non-complex (monophase) variables. The complex conjugate symmetry is thereby split and the existence of the so called "spin" is made manifest in individual wave modes (though spin involves also paired components of frequencies, and that will be discussed later).
The expressions for charge and current densities negate with relative time reversal. The oddness of the Hilbert transform kernel function (which for relative time reversal does not reverse) sees to this. This is consistent with anti-matter being reality-convergent in reversed time since negation of its real part is required in order to maintain the convergence.
We might feel concern over the way that these deliberations about charge involve only the time dimension and lack the usual relativistic symmetry across the four dimensions of space-time. However the basic Planck relationship between frequency and energy for quanta is also asymmetrical in this same way, so we appear to be discussing an issue that is properly specific to the time dimension. See Appendix E for further discussion of this.
Separation of the handling of terms at different temporal frequencies is rather more intuitive and convenient in the one dimensional frequency (Fourier or Laplace transform) domain than it is with time and space remaining as represented in a four dimensional partial differential equation. This can be readily understood by visualising the atom in its four dimensional space-time using the natural units. For all practical time periods between, and even within, state transitions the atom is much longer in the time dimension than in any space dimension, and is also strongly periodic along the time axis. Even for a state duration of 10-15sec the atom is still some thousands of times longer in time than its equivalent width in space. Writing this in spatial Laplace transform form would require a convolution in the spatial frequency (wave vector) domain. However the inter-term products of differing resonant frequencies are relatively small and for many purposes (e.g. electrodynamics) have little significance. In particular these high frequency cross terms converge rapidly with increasing frequency, and this justifies the use of the Hilbert transform in the time domain representation because convergence of this integral in the frequency domain shows that the evaluation of the time domain function converges to local dependence as the bandwidth of the evaluation is increased.
So freed from any severe problems with these high frequency terms in our electrodynamics mission and presuming steady state ("eigen" conditions) with
| Echarge |
See Appendix C for a discussion of how physical phenomena relate to this formulation of charge and current origination.
See also Appendix F for comments regarding the involvement of modulus and sign of frequency in these expressions.
The variables
From the above expressions the electromagnetic field strengths may be derived in terms of a Huygens wave integration of all the sources over space. Here is an expression based on speed of light Maxwellian propagation delays:
| E5 |
Note the divisions with vectorial divisor and a dividend that is scalar in the electric case and vector in the magnetic. For a description of the form of this operation and further notes on the meaning of this please refer to Appendix D.
These equations define the Maxwellian system of coupling wave propagation in free space for near fields. We can use the free space form because our model includes the sources that would create or disturb any such waves. Screening and increase of refractive index occurs through the interaction of matter in the propagation path. It is no more than the presence of an interactive response term in the matter that acts to scatter, reflect and delay the incident Maxwellian wave.
These propagation formulae showing an inverse square law of magnitude with distance are suitable for near field, that is where the distance from origination to the influenced field is small compared to the wave radian length. This is usually valid for the cases of optical waves and nearby atomic or molecular interactions. However, for very far field effects (Fraunhofer field) the relationship changes to magnitude inverse with distance (conservation of spherically integrated intensity). In cases where either the source or influenced structure operates conherently over a space greater than the wave radian length then for intermediate distances (Fresnel field) greater than the radian length an extension of the near field coherent effects occurs so that these formulae may then remain valid there.
For atomic structures the propagation delay of field perturbations is very small in relation to the periods of state evolution (i.e. in relation to the reciprocals of real parts of the system poles), so the time delay terms can usually be omitted for these cases and a simpler prompt model can be used instead.
| E6 |
Regarding the vectorial divisions, as was the case for E5, for a description of the form of this operation and further notes on the meaning of this please refer to Appendix D.
To set up the nuclear charges upon which to base simple electrodynamics models equations E5 or E6 can be evaluated with the requisite fixed concentrations of charge located at the desired nuclear centre(s) to be added to any fields produced by the electrons via the charge and current formulae EHt or Echarge.
The combination of the Klein-Gordon equation governing electron wave and the charge origination formulae with Maxwell equations for propagation of electromagnetic field stress is the complete definition of the electrodynamics model as used here. Our purpose is now to explore features and properties of its dynamic behaviour in the vicinity of atomic nuclei (but not inside those nuclei ... that remains for further extension work on the model).
 Charge Quantisation
Charge Quantisation
We now set out to describe both structurally and quantitatively the way in which the continuum charge in the electron fields of atoms, molecules and crystals becomes organised so as to behave in quantal units.
Let us define unit charge origination as that occurring in a cube of unit edge containing a volumetric average unit intensity at unit temporal frequency. Looking at this in spherical polar co-ordinates we may define that when in isolation the potential at the surface of a sphere with radius r that is concentric with and contains such a (cube defined) unit charge is
The latter Cartesian arrangement is more in keeping with the SI system of units (though, oddly enough, the 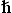 = c = me = z0 = 1
= c = me = z0 = 1
Regarding units of charge in the basic scheme used herein:
If, all in basic (hypothetical) units, the Cartesian cuboid definition of charge unit has value 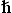 /z0)
/z0)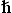 /z0)
/z0)
Quantal behaviour occurs in phenomena of both the original charge and the original magnetising current kinds and they are both produced in the same type of wave field. The charge quantity is connected with the number of half wave ripples in a real wave (with actual zero crossings) along a path starting at a positive nucleus and ending by tapering away at great distance, and the magnetic quantisation is connected with the number of ripples (or rather, argument rotations of a complex variable having no zero crossings) along a path that forms a closed loop.
For an initial grasp we can concentrate upon the charge phenomena alone. This will allow us to make non-relativistic approximations whilst we come to a picture of the "orbitals" surrounding static structures of atomic nuclei. We shall then be in a position to augment this picture with the quasi dynamics of wave-orbital magnetic effects whilst still avoiding total generality, but with a view to how this might then be generalised by various forms of perturbations, both static and dynamic, for yet further extensions of validity of the working approximations.
It is in the exponential nature of the solution of a partial differential equation that separation of multiplicative factors in the solution corresponds to the separation of additive terms in the differential operator. Thus we may consider factorising the solution wave of any given such equation in terms of the product of some factor wave corresponding to a restricted set of operator terms and another wave function determined by the residual part of the differential operator. For certain cases this yields useful properties in the parts so separated. However, there are interaction terms to be taken into account between the two factor solutions.
For a bound multi-electron wave field it is possible to extract from the system differential operator a term in the second spatial derivative plus any and all of those terms that result from charge density and thereby associate with electric field divergence. This can also be done in a way that is independent of the eigen-frequencies of the individual electron mode fields, and then the only interaction effects to allow for act in the one direction from this extracted term into the various residual electron modes. A truly independent factor can be established that depends only on the aggregate charge distribution, not specifically on the individual electronic modal forms. So an independent factor wave of this sort can be seen as instrumental in regulating the charge equilibrium of the ensemble of electronic modes.
Since we are seeking a steady state (oscillatory) solution for these electron waves this equation need only embrace the three physical dimensions and not time. This can then be arranged to create a second order partial differential equation of Helmholtz type. It can be guaranteed to have a real solution (sum of paired complex conjugates) so long as its coefficients are also all real. If we can get its conditions to correspond to the requirements for stable field operation then the solution of this equation must be a factor common to all of the electron wave modes that are contributing to the local charge density.
By avoiding the inclusion of first order terms in the common factor equation its solution will be a static real wave function that we may view as the sum of a pair of constant amplitude complex conjugate terms. The angular argument of these two complex terms will then rotate with increasing distance from a nuclear charge centre. After rotating at various rates as a function of distance they will converge to some constant value at large distance. In order that the rotation shall cease at great distance it is necessary that the non-differential term in the equation shall converge sufficiently rapidly to zero at that great distance. There is a similar convergence requirement on all of the electronic modes present.
Given the above conditions the solution of the common factor equation will then be a real sinusoidal wave with period varying along the path from nuclear charge centre to some field zero surface at great distance. To enforce a zero at the nuclear origin and also at this great distance the complex conjugate pair of terms must sum to zero at both of these points. For that to be the case requires that the argument of each complex term shall change by an integer multiple of π from the origin to the distant point of zero field.
We can, in fact, find a partition of the differential operator corresponding to such a common factor, leaving everything else in the residual equation governing the individual electron modes. It remains then to show that the quantisation effected by this partitioning is unique (see below) and produces equality of the resulting quantal sub-divisions of the charge. This method of factoring has then converted the solution of an equation with divergence in its vector differential coefficient field to the product of two functions defined by equations neither of which has such divergence. This simplification is useful.
The spatial frequency of the two complex conjugate solution terms of the common factor equation vary as the square root of the ratio of the non-differential term to the coefficient of the second order differential term in the equation. Our task is to show that this ratio is suitably related to the charge density distribution as to imply quantisation to a universal quantum. We may use the fact that the divergence of the electric field is everywhere equal to
Thus we may be able to show that there is a process by means of which the charge can be regulated to an integral multiple of a fundamental quantum in the aggregate electron field between nucleus and a far field zero. Also it is apparent that the quanta of charge in the system will be segmented into regions separated by surfaces at which the aggregate charge density goes to zero. These surfaces of zero density are additional to any zero intensity surfaces involved in the individual electron modes making up the aggregate field. The quantisation applies to the overall charge structure, but not to that in the individual electron resonance modes.
Using this model as indicated below produces a value for the fundamental electronic charge that is close to the observed value. We are then left to consider what corrections might be applied to that figure.
About the wave equations:
Here are examples of the Modulated Klein-Gordon (MKG) equation with the units scales, including charge, explicit in their conventional form and omitting the magnetic terms as unnecessary for a simple static model of an atomic system. This omission would affect resonant frequencies (c.f. Lamb shift), but not the value of the charge quantum.
We could (but I do not) use the Cartesian MKG equation to define an electron wave system that is structured only by the Coulomb potential of a nuclear point charge at the origin. That would be reminiscent of the potential notion of a Lagrangian model giving a conservative field where energy level for a charged particle would be a single valued function of spatial position. Such an equation, having the spherically enclosed charge q as merely a function of spherical radius
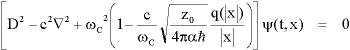 |
E7 |
That sort of equation can yield eigen functions that are broadly similar in frequencies and spatial geometries to what follows, but it omits some essential form, and in particular it does not quantise spontaneously. It is a second order version of the usual first order temporal differential Schrödinger equation model for a single atomic electron mode.
For the electrodynamics modelling purposes of this essay we stay with a point centric approximation for the nuclear charge, but we add the effects of distributed charge of the electronic waves themselves throughout the space that they occupy. We can introduce these effects via the coefficients of the second order spatial derivative terms as a tensor matrix that ultimately reduces in its effects to the magnetic vector potential
For simple steady state cases only (continuous oscillatory and no externally applied fields) we may introduce the effects solely via the non-differential term in the equation. When this is done the requisite function  ·u(x)
·u(x)
So we can then write the Cartesian Modulated Klein-Gordon (MKG) equation with distributed charge density equal to the divergence of the electric field as:
[D2 − c2 2 + ωC(ωC − c.div u(t, x))] ψ(t, x) = 0 2 + ωC(ωC − c.div u(t, x))] ψ(t, x) = 0 |
E8 |
Remember however that we are working here below with the charge in basic (hypothetical) units of 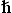 /z0)
/z0)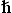 = ωC = c = z0 = 1
= ωC = c = z0 = 1
I shall for general purposes later use the wave equation written in terms of the field strengths. For the electric field these are the gradient of potential, and for magnetic effects they are the so called "vector potential". However for evaluations limited to the steady state (steady oscillatory) condition a compact form of the wave equation written in terms of charge density
[D2 −  2 + 1 − div u(x)] ψ(t, x) = 0 2 + 1 − div u(x)] ψ(t, x) = 0 |
E9 |
Note that if we could remove the dependent variable charge term in E9 then that equation could take the Helmholtz differential equation form. So we attempt this by setting up the wave variable as the product of two independent wave functions. We then have the opportunity to collect the differential terms of the product in such a way that the effects of the distributed charge appears through
Seen this way the process is bilinear. We shall break it into two linear processes, each depending for its form on the other, with the two sub-processes thus forming a circular causal loop. One of these processes describes the distinguishing part of the complex variable motion of any one individual electronic mode, we may call it
For electrodynamics modelling this is an attractive proposition because the periods of the electronic oscillations are very much shorter than those of the charge fluctuations, so the aggregate charge effects act like a nearly constant structure controlling the form of the individual electron mode waves. Also the charge distribution is formed as the sum of the individual electronic modal charge distributions each of which displays the smoothness described above, i.e. they do not oscillate at double frequency in their self quadratic effects as a Lagrangian model would tend to suggest. Further this aggregation of mode charges tends to remove the effect of charge fluctuations by averaging, especially for heavy atoms or high order modes in molecules, crystals etc. (Compare this simplicity with the difficulty of the modelling approach through the "many body system" concept under a Lagrangian particle model.)
To clarify the type of equation we are about to use first consider these basic forms of differential equations describing a three dimensional scalar field. We omit time from this discussion since it will be taken care of in the other equation of the pair, and indeed is reduced in effect to a complex constant for the steady state oscillatory solutions:
 2 y(x) = 0 2 y(x) = 0 |
 2 y(x) + f(x) = 0 2 y(x) + f(x) = 0 |
[ 2 + k] y(x) = 0 2 + k] y(x) = 0 |
[ 2 + f(x)] y(x) = 0 2 + f(x)] y(x) = 0 |
It is the modulated Helmholtz (MH) form of equation that we shall use to carry the effects of the irregular charge distribution as a factor in the model. We can take a look at some properties of the waves that are its solutions.
We shall be particularly interested in those cases of the MH type of equation where the modulating coefficient function
| d2ln(y+(x))/dS2 + f(x) = 0 ?? |
This looks like a one dimensional Poisson differential equation in the log of the wave function with a real function of space as the source term.
If there exists another function  ·u(x) = f(x)
·u(x) = f(x)
 y(x) = u(x) − u0(x) y(x) = u(x) − u0(x) |
By treating
So what is this special part of the electric field
The solution of this real scalar MH equation in three dimensions is dependent only upon
In order to demonstrate that quantal resolution must occur within the model propounded here we shall need to show that due merely to the properties of the MH equation the rate of rotation of the argument of
There is more to go in here for developments of proof of the above conjecture.
Using a construct of this MH sort the following procedure extracts the effects of charge as a separate factor with ripple form, leaving behind a residual equation for each electronic mode that, although subject to ripple distortions due to the separated charge factor, still has a linear wave equation form. This relies upon the effect (a constitutional necessity when the equation is factored in this way) that the zero surfaces of ripple caused by the common charge distribution shall be identical for all modes. There can be additional zero surfaces in those modes having principal quantum number
Consider a factor differential process that produces ripple with zero surfaces that partition the charge spatially. This will only produce the correct results if the actual modal distributions are also calculated and used, and the execution of such a calculation is a recursive procedure. However, for the purpose of deducing the magnitude of quantal charge segmentations by the ripple the reasoning can be based upon the phase of the ripple itself. So long as this can be shown to segment the charge in a manner that is invariant over the space of possible electronic modal forms in all their additive combinations then the basis for constant levels of quantisation may be thereby established without resort to the calculation of actual modal distributions or relative excitations. Given such invariance the ripple function can be separated as a factor common to all electron modes in the given atom, molecule or crystal. Only the total charge origination will then be of importance, and is in any case all that is relevant to the quantisation proof.
Such a ripple factor process will require that the qualitative properties at its boundaries regarding charge state attractor stability and convergence lead to stable quantal charge operation. It is this which determines the permitted stable states of ionisation. The outermost zero surface of the ripple for ionised structures will take the form of amplitude convergence as the first order exponential of distance (quadratic exponential for convergence of wave intensity), or to a higher (exponential) order of exponential convergence for electrically neutral structures.
We could establish a picture of the quantal formation process by means of the scalar modulated equation in E9 converted into spherical radial co-ordinates, and that has a certain attractive simplicity. However, the interpretation of deviations of the structures from pure spherical symmetry and the generalisation to dynamic situations are not then readily evident. So I shall use the more general form of the wave equation here in which the coupling terms appear only as field strength coefficients in the elements of a differential operator coefficient matrix. This approach has the further advantage that it can be used in a similar form for derivation of the magnetic quantisation process where a simple potential function cannot in any case be used. Unfortunately this way the one dimensional radial form of the especially simple (near) spherical symmetry of atomic cases is not so readily visualised and needs a little more thought.
Many issues herein could be expressed very compactly in tensor notation, but our mission here is topological comprehensibility and not conciseness or mathematical generality for its own sake. Instead I shall mostly adhere to the layman's sense of distinctness between time and space and treat the co-ordinates as a compound
Such a
Thus the separation into time as a scalar real variable and space as a
Because we need to use both four dimensional expressions as basic definitions and three dimensional expressions where static approximations occur we need to make sense of the distinction between the respective differential operators. First we combine the  differentiations into a single four dimensional operator denoted by the lozenge symbol ◊. I avoid here the square symbol
differentiations into a single four dimensional operator denoted by the lozenge symbol ◊. I avoid here the square symbol  called "box" or "squabla" because, at least sometimes, it is used to represent specifically the Minkowski four dimensional second order differential operator ... the d'Alembertian. By embedding constants in this ◊ operator (and, indeed, also in D and
called "box" or "squabla" because, at least sometimes, it is used to represent specifically the Minkowski four dimensional second order differential operator ... the d'Alembertian. By embedding constants in this ◊ operator (and, indeed, also in D and  when necessary) the time and space units can be normalised. So we use
when necessary) the time and space units can be normalised. So we use
 ] { ≡ τC [∂/∂t, c.∂/∂x, c.∂/∂y, c.∂/∂z]in practical units} ] { ≡ τC [∂/∂t, c.∂/∂x, c.∂/∂y, c.∂/∂z]in practical units} |
Eloz |
Using this symbolism the second order Minkowski differential operator (the d'Alembertian) can be written as  ≡ ◊T·M·◊
≡ ◊T·M·◊
|
Emink |
For cases where we wish to analyse a system that can be described as linear with constant or perhaps very slowly varying parameters then to achieve improved separability of its dynamic terms we shall wish to express it in terms of the frequency domain transform of its wave variable. Thus a complex wave variable
In the case of slowly changing linear systems then the system dynamic coupling coefficients can be treated as being slowly varying functions of time, and the analysis can follow as a slowly perturbed result derived from the steady state behaviour. The restriction to "steady state" includes the cases of multiple modes each in steady oscillatory motion. The question of how slow is "slow change" then rests upon whether the (eigenvalue) variable
Hybrid Differential Operators:
To allow expressions corresponding to differentials treated symmetrically over space and time (as is typically done in relativistic considerations), but using the frequency domain for the time dimension, we shall need a hybrid form of the differential operator. Thus a frequency domain hybrid lozenge operator
 ]T ≡ τC [s, c.∂/∂x, c.∂/∂y, c.∂/∂z]T ]T ≡ τC [s, c.∂/∂x, c.∂/∂y, c.∂/∂z]T |
ElozF |
In this hybrid operator the first element operates multiplicatively upon the elements of left or right entities whilst the remaining differential elements operate each as though convolved with elements of its operand that is the neighbouring entity immediately to its right. In this latter respect we consider a differential here to be the integral of the operand weighted by a smooth doublet function centred around the given coordinate value, with unit moment, that is then taken sufficiently close to its narrow limit to be valid. So the first element of the hybrid operator commutes with elements to left or right which are functions (i.e. not differential operators), but the differential operator element, although in succession of differentiations still commutative over the same or anti-commutative (sign reversal) over different independent variables, cannot commute with its operand function that is to its right.
We may write a generalised form of the complex scalar Klein-Gordon partial differential equation with added coupling terms in both the space-space and the mixed space-time derivatives as:
| Ekg |
I plan to work with the time dimension in the frequency transform domain whilst keeping the space dimensions untransformed. Transforming all of the dimensions or none would also both be possible, but the hybrid arrangement is in many ways more convenient for visualisation. We effectively think of the problem in terms of one component temporal frequency at a time along with its respective explicit physical spatial wave function geometry/topology. We use
So we can write the hybrid frequency domain form of the equation for the
| EMHM |
Then the hybrid frequency domain description of the full wave function is:
|
EMHS |
We may then dissect and define the parts of this matrix A as follows:
|
EmatA |
|
EmatW |
Note that the overall matrix A is Hermitian, i.e.  Ψ
Ψ
Further development of the model regarding the origins and more general behaviour of this vector u and matrix W is possible, but for the purposes of the derivation of a quantisation model this description is sufficient. I shall defer enunciation of the simplifications it involves for a separate presentation ... see Dynamics of Complex Waves. However it is worth noting that the division by
Working in one particular temporal frequency with steady values of u and W replaces the modulated Klein Gordon by a modulated (and spatially damped) Helmholtz equation. So expanding the terms in EMHM above we may write this Helmholtz equation for mode n under the effects of the total charge from all modes as:
[ T·{(I + W(x))· T·{(I + W(x))· } + (u(x) + u*(x))T· } + (u(x) + u*(x))T· + ωn2 + ( + ωn2 + ( T·u*(x)) − 1] Ψn(s, x) = 0 T·u*(x)) − 1] Ψn(s, x) = 0 |
E10 |
Note particularly here that the differentiated product  T·(u*(x).Ψn(s, x))
T·(u*(x).Ψn(s, x))
 T·u*(x)
T·u*(x)
Now we collect the elemental differential terms, noting that  T·u(x)
T·u(x) T·W(x)·
T·W(x)· = j2
= j2 T·(v(x)T×
T·(v(x)T× )
)
| Emode |
Under some conditions we may take advantage of the vector identity  ·(v(x)×
·(v(x)× ) ≡
) ≡  ×v(x)·
×v(x)· + v(x)·(
+ v(x)·( ×
× )
) ×v(x)
×v(x) ·(v(x)×
·(v(x)× Ψ) = a(x).
Ψ) = a(x). Ψ
Ψ
The model includes no explicit expression of field induced from outside of the closed causal structure of the system being described. These are, of course, the Maxwellian real vectorial fields that are the basis of electromagnetic phenomena. It is indeed possible to add electric and magnetic field terms that are arbitrarily imposed, subject to their Maxwellian form, that result from charge and current structures outside of the system being directly modelled. These electric field and magnetic vector potential field strength terms add respectively into
Since such remotely induced fields can have no divergence because they are not associated with local charge or current they do not affect the term in  ·u(x)
·u(x) ·(v(x)×
·(v(x)× Ψ)
Ψ)
The most simple and important cases of externally induced fields to be considered are those that are essentially of uniform stress in a single spatial direction throughout the model, and either constant in time or subject to an oscillatory modulation that may be described in terms of their frequency domain spectra. To check the validity of the equation Emode as a model of testable physical phenomena under these sorts of fields we may investigate its compliance with observed spectral absorption and emission effects and Stark, Zeeman, Paschen-Back and Stern-Gerlach effects as outlined in Appendix C.
We substitute a product of factors for the wave variable as
H(x, t) is the real ripple factor common across all modes, static or a slowly varying function of t,
Gn(s, x) is the residual complex high frequency factor for electron mode n.
Please refer to Wave Topology of a Spin Mode for further detail on the form of the spin mode-factor.
We can now partition the differential operator terms into groups corresponding to these factors to produce a form of separation of variables. Let us for the time being leave each
We might describe this model as having "stochastically separable variables". It is justified because for a wide range of electrodynamics problems the temporal frequency spectrum of the modal form corresponding to
In response to any challenge to the validity of this form of approximation involving different orders of dynamical rates of change or of widely differing frequency bands, we may counter with the defence that the notion of "quantised variable" depends upon a concomitant notion of "steady state". In the states of transition between what we think of as steady states the meaning of quantal value is in any case severely weakened. At best we then have an underlying continuity and conservation of charge (and something corresponding for the magnetic effects). We are bound to approach considerations of quantal phenomena in terms inevitably somehow related to what we call "steady states", and allowably also their weak perturbations.
Further, we know that the
Leaving as a built in part of each individual electron mode its own spin factor but separating out the ripple factor
[ 2 + 2u(x)T· 2 + 2u(x)T· + j2 + j2 T·(v(x)T× T·(v(x)T× ) + ωn2 + ( ) + ωn2 + ( T·u(x)) − 1] (H(x).Gn(s, x)) = 0 T·u(x)) − 1] (H(x).Gn(s, x)) = 0 |
E10a |
... where
HG″+2H′G′+H″G + 2u·(HG′+H′G) + j2 ·(v×(HG′+H′G)) + (ω2 + ·(v×(HG′+H′G)) + (ω2 +  ·u − 1)HG = 0 ·u − 1)HG = 0 |
E11 |
So we next select a set from the terms in the zero differential order of
H″G + ( ·u)HG = 0 ·u)HG = 0 |
E12 |
Notice regarding E12 that if the terms in the first spatial derivative of H containing u and v were included here it would alter the way that this equation determines the fields so produced, but any such states for the model will drift under thermal interactions until these first spatial derivative terms vanish. As an alternative choice of this sort we could include the terms in the first derivative of H as shown in E12a.
H″G + 2u·(H′G) + j2 ·(v×(H′G)) + ( ·(v×(H′G)) + ( ·u)HG = 0 ·u)HG = 0 |
E12a |
The function H may take different forms under the presence of differing amounts of these terms so long as the
Thus it becomes clear that the pure second derivative Helmholtz forms of the H equation are locally lowest energy solutions for the electronic system in the continuum space of possible H functions. Any amplitude deviations of H from a simple modulated Helmholtz ripple form caused by non-zero terms in the first spatial derivative can only be transient solutions, because net energy radiation occurring in thermal interactions (how fast?) will succeed in bringing the system state toward its minimum energy. In this process the H function will transition smoothly via various continuum states along with corresponding smooth changes to the
So using E12 we write, with modulated Helmholtz form, a
| Eripple |
The above equation leads to  T·u(x)
T·u(x)
From this we may seek to establish an equation applying to a contour S following the direction of vector  |Ψ(s, x)|
|Ψ(s, x)|
Note that equation Eripple is not based solely upon electric potential
For a given
Collecting the remainder of the original abbreviated product derivative terms we have:
HG″ + 2H′G′ + 2u·(HG′+H′G) + j2 ·(v×(HG′+H′G)) + (ω2 − 1)HG = 0 ·(v×(HG′+H′G)) + (ω2 − 1)HG = 0 |
E14 |
Dividing through by H this produces an "Electron Residual Equation":
| Eresid |
... where  H(x)) / H(x)} ≡ {(sign(H(x))).
H(x)) / H(x)} ≡ {(sign(H(x))). ln|H(x)|}
ln|H(x)|}
From equation Eresid it can be seen that the dynamics of each electronic mode are linear with spatially varying but temporally constant parameters so long as the function
As a consequence of this, and also on grounds of necessary smoothness in the solution of Eresid at the origin, we may deduce (perhaps with some surprise) that every Gn wave function assumes a constant non-zero value at the origin. Presumably there is some corresponding constraint on the form of these functions at the periphery (what is it?).
Because equation Eripple has modulated Helmholtz form in three dimensions, the integral of charge density over each region that is bounded by zero surfaces is constant. We need to establish this by proving that the solution is always an irrotational field (Gauss' divergence Theorem or the Poincaré lemma could be invoked here). It can be approached by considering how:
- a) The zero Laplacian in three dimensions (and only in three) acts to modulate the intensity with a gradient that is normal to and inversely with curvature of the local isopotential surface (that is a mathematical idea of potential applied to the wave function, not the electrical potential as integrated from a Maxwellian electric field ... it is not an energy potential). Thus only enclosed sources change the surface integral of intensity over any equipotential surface.
- b) The rate of phase rotation times the squared cosine of that phase for each complex conjugate solution is proportional to the local intensity of the oscillatory solution.
Note that positive charge contributes negative local second derivative to the potential gradient.
A similar form of reasoning then has to be used to establish the value of the quantum of magnetic field flux. I hope, in the fullness of time, to add it here. It is interesting to note from Emode or Eresid that the way
 The Fine Structure Constant
The Fine Structure Constant
The quantal unit of charge in conventional units is expressed as 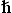 )/z0)
)/z0)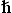 )
)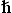 /z0)
/z0)
There are three places where the "
- The consequence of spherical integration in equation E5 of field generation by the originating charges and currents.
- The definition of the basic unit of charge where it appears under the square root as multiplying Planck's
constant .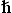
- The ratio between the two alternative basic charge unit definitions
qC andqS .
In the first of these, because the field produced propagates in all directions of the three dimensional sphere, the divergence this produces is multiplied by this factor. The second arises in either of the equivalent integrations EHt or Echarge and also corresponds to the way it appears conventionally in the relationships between the electronic charge and the fine structure constant. The last of these three is not of any absolute significance because it is only a matter of convention, and if it is used then still its effects must cancel in the different parts of the model.
We must now apply the following principle before we can calculate the fine structure constant:
Recursive Observation Lemma: Any general theory of observable reality that is valid for an observer must be valid in accounting for the processes in an observed observer.
The topology associated with charge quantum regulation introduces a further change of scale, so further rescaling to the conventional effective units will be necessary because it is only the quantum charge unit itself that is absolutely defined, not the length or time scales that we choose for the original model. We have deduced that the charge on each Klein-Gordon electron will be multiplied by a factor determined by the ripple phenomenon. It is this that will need to be brought into the issue of scaling of units.
To set up the proportions of the system we use the static ripple process equation Eripple. We can take advantage of the conformal properties of the solutions of the Helmholtz equation. These are still true even in its modulated form. Because of this we may ("without loss of generality" as they say) evaluate this factor by resort to the simple case of charge per unit thickness in a thin spherical shell wall at unit radius. The logic is applied for just one of the two complex conjugate components making up the real ripple wave.
The following logic is not self-evidently accurate, though it is at least approximately correct in the value of the fine structure constant at which it arrives. An improved account is being worked on, and what is sought is a proof that the charge quanta that are subdivided by the zero charge density surfaces are indeed all of equal magnitude.
Suppose a single complex wave component of the real solution of the ripple process equation Eripple has a uniform unit charge in the basic Cartesian hypothetical units per unit thickness of the shell wall (i.e. a total charge of one hypothetical unit
Thus the enclosed charge between adjacent zero surfaces, being one quantum, is increased in the ratio
This means that in the spirit of the Recursive Observation Lemma all possible electron quanta we might use for observations have already been increased in size by ripple effect in the ratio
This has been evaluated with no allowance for the possible effect of the spin mode topology, so a further correction for that might yet be necessary (work ongoing). However the discrepancy of a slightly too high value for the fine structure constant (and correspondingly of the charge quantum value) also may form part of the basis for a further development of the model, including in the matters of atomic nuclei referred to as quantum chromodynamics.
 Discussion
Discussion
Ionisation.
It is necessary to recognise that the same form of ripple process equation Eripple will solve for the different H functions corresponding to different ionised states. It can do this due to the recursive effect of the H solution carrying with it its own respective collection of variously excited electron modes and their consequent distributions of charge density contributing to overall quantal determinacy.
In setting up the equation Eripple there is a step at which terms from amongst those depending upon electric and magnetic fields are selected for separate treatment. Clearly the term containing the divergence of the electric field, since it defines the charge density, must be included in total if the function H is to have the quantising properties we need. But regarding the other terms, we might set out by thinking of the difference in their treatment as just a choice on our part, that they may appear in the equation defining H or just as effectively in the residual part contributing to the form of the individual electrons. We are apparently free to include or exclude these extra terms so long as they involve
As regards the possibility of taking some or all of the unit constant and the
So what is it that determines this choice of terms contributing to the two sorts of factor fields? It is just that H can only lead to the lowest possible energy state of the electronic structure if the ripple equation has zero coefficient for its first order spatial derivative terms. So all of the different ionisation states of the structure must be found with the one form of the equations.
There is only one choice that will bring the
 Appendices
Appendices
For additional work here:
Ref out to phenomena explanations e.g. cloud/bubble chamber tracks, Compton effect etc.
Appendices:
Refutation of particle presumption in Shimony et al
 Appendix A: Statistics and the Lagrangian Model
Appendix A: Statistics and the Lagrangian Model
Add notes here comparing the conceptual stances of Lagrangian and Eulerian time/space dynamics models.
The power or energy spectrum of a real scalar function of time is expressed as a real scalar function of frequency. We can get to this function in terms of an original wave either by filtering in narrow bands then averaging squares of magnitudes or by correlating across different time intervals and then Fourier transforming the result ... they lead to the same power spectrum. That is a rough expression of the "Wiener-Khinchin theorem".
We may call this a "first order spectrum". Higher degree functions forming further first order statistics are also possible, as typified by the moment functions, though we shall not need them here. Also we should perhaps call this a "self spectrum" in the sense that it is restricted to include multiplicative interactions only between the values of the single original wave, i.e. it is characterised totally by the autocorrelation function of the original scalar wave.
When this idea is applied to a spatio-temporal wave then it is necessary to take account, and still at this first order of statistics, of the more extended set of self and cross-correlations between the local derivatives at any given point. In four dimensions there are sixteen of them, each obtained as the average of the time-shifted product (note a particular precedence given to the time dimension at this point) of a particular pair of first partial derivatives.
Processes of observation are built upon local fluctuations of energy or power. The study of the results of these fluctuations as applicable in observation requires the use of statistics that are of at least a second order (i.e. they are statistics of statistics) in relation to the original waves. When short term wave samples are used to estimate or measure such a first order spectrum in a multi-dimensional spatial context the fluctuations can be analysed in terms of second order spectra that will depend not only upon the first order self spectra but also upon the inter-dimensional correlative form of the waves. When, as turns out to be the case, we are dealing exclusively with second derivatives (that is a relativistic requirement) then these first order correlative cross-spectra can be expressed in terms of correlation functions of the derivatives over mixed pairs of dimensions. For the study of dynamics we are particularly interested in those terms that involve the pairings of time with each of the three spatial dimensions.
When they are derived from a system of real variables (as is done in the Lagrangian model) then a feature of these second order statistics is that they necessarily involve greater bandwidth than the first order statistics to which they are related. This can be understood in terms of treating the real variables as sums of additive complex conjugate terms. It is a consequence of the interaction of these terms with equal and opposite signs of frequency. They produce terms in the product at the sums of moduli of frequencies. These sums must extend to higher frequencies than are found in the original waves. That spectrally dispersive sort of process yielding higher frequencies, especially in an engineering context, is often called "up conversion".
There are systems of complex variable waves that are not necessarily subject to this inherent expansion of bandwidth in the second order statistics. These quieter complex variable systems are not amenable to analysis by the Lagrangian model of dynamics, or at least, not without inordinate amounts of redundant additional structure to cancel out the irrelevant up conversion effects. This can be expressed in terms of the fact that the paired conjugate variables of the Lagrangian system cannot be made to satisfy the Cauchy-Riemann condition of differentiability. Whereas the position/momentum co-ordinates are validly related to the Lagrangian model only in a particular rotational orientation in their phase space, the real/imaginary parts as the complex co-ordinates are valid vis-à-vis complex differentiability for any rotation in the complex plane. The complex system displays a relativity of complex argument (and therefore smoothness with respect to phase) whilst the Lagrangian model always produces absolute effects of phase. It might be possible to use two Lagrangian models constrained to meet this requirement of rotational smoothness but that is a redundant and pointlessly complicated form of modelling.
One might wonder what has happened to the invariance producing effect of the potential function of the Lagrangian model that is dispensed with in the complex model. The answer is that all such energy related effects emerge solely from the operation of the wave equation. If that were not the case then there would remain little point in entertaining such models. Also, with the exception of limited special arrangements to handle spin, all approximations can be made using only analytic functions so that complex differentiability is maintained. The potential function is not imposed. Instead it emerges as observable in certain ways from the wave process.
A conventional way to approach the analysis of complex scalar waves is to consider them in terms of the real and imaginary parts separately, and this is sometimes done. However, that does not bring out the effects of any inherent correlation between these two parts, and in particular, any negative correlation that could act to reduce the overall intensity of fluctuation or "noise power" below that of the case with uncorrelated real and imaginary parts. The result is too "noisy".
 Appendix B: Three Wave Couplings
Appendix B: Three Wave Couplings
Reference should be made to Allen and Eberly [AE87] "Optical Resonance and Two Level Atoms".
There is more to be said here yet, but here is an outline.
When an electromagnetic field is present with a pair of electron modes then couplings between the modes occur if they have opposite spins. For a given phase relationship between the two modes one will gain energy whilst the other loses.
Thus it is possible for a pair of complex De Broglie waves to interact with a single Maxwellian electromagnetic wave. The Maxwellian wave is real. (Add a note here about the "Bloch-Siegert shift" (see Allen and Eberly [AE87] pp47-50).)
The electron fields in an atom or molecule already affect each other by virtue of their intensities and this maintains the physical structure of the atom, but otherwise (i.e. by their phases) they do not significantly interact directly. Hence we are particularly interested in these triplet interactions made of two matter wave modes and an electromagnetic wave because they are the chief basis of changes of modal excitation states.
When the interaction is between two modes that are similar except for opposite spins then there is no frequency difference and transfers of energy can be induced by a steady magnetic field (Zeeman effect) and with no net radiation or absorption of electromagnetic energy. The state changes involving the two modes then perform cycles that can be described in a three dimensional energy/phase state space that is referred to as a "Bloch space". These energy fluctuations are referred to as Rabi processes. They appear as line splitting in the radiation absorption and emission spectra of the atoms that are within the steady magnetic field.
If a pair of modes are considered with differing frequency, with opposite spins and also differing in modal form so that their product is a dipole then similar energy interchanges occur so long as the electric field is reversed with a frequency to match the reversals of phase between the two modes, that is, at the difference of the two modal frequencies. Again a Bloch space model with two energy dimensions and a phase can be built to describe the state gyrations. However, in this case there will be electromagnetic energy emitted or absorbed to make up the balance as transfers between the electron modes occur with powers proportional to their respective frequencies.
More material explaining and quantifying this model is needed here.
 Appendix C: Charge, Current and Physical Phenomena
Appendix C: Charge, Current and Physical Phenomena
There is an unfortunate clash of nomenclature regarding the term "azimuthal" as inherited from the conventions of twentieth century quantum mechanics. In talking of spherical systems with an axis it is proper to use the adjective "azimuthal" to describe patterns, positions and angles in the equatorial plane of the system. In pursuits such as gun aiming and also in wave systems such as are described in antennas and resonators this convention is the one used. Thus the azimuthal order of a spherical harmonic is most naturally associated with the number of cycles of the variable occurring in a circuit around the axis. The harmonic order constituted as the number of half cycles of the variable along the latitude angle from pole to pole would then tend to be referred to as the latitudinal or possibly the axial order. The remaining spherical order is then the radial, being the number of half cycles in the radial form from centre to periphery.
Unfortunately because of the early observation of magnetic quantisation in isolation the term "magnetic quantum number" denoted by
Meanwhile, as a result of spinning top momentum models the term "azimuthal quantum number" (alternatively called "orbital quantum number") denoted by l (letter L) then became associated in a rather complicated way with what in a wave model would be called the latitudinal (axial) harmonic order of the wave mode. Here we define the axial harmonic order as the number of half waves along the entire latitudinal angle and denote it as
As a further point of detail, the principal quantum number is often loosely thought of as the radial order. That is not true. Rather it is what it would be if the other two orders were at their minimum absolute values
Recalling from the above text we may take the densities of electric charge and magnetising vector (i.e. electric current) as generated by the following formulae:
| Echarge |
Recapping also the electron mode we have a basic picture:
| Emode |
| Eresid |
... where  H(x)) / H(x)} ≡ {(sign(H(x))).
H(x)) / H(x)} ≡ {(sign(H(x))). ln|H(x)|}
ln|H(x)|}
For the circularly uniform orbitals with
In spite of the absence of a spontaneous magnetic dipole for the  Ψn ≡ j
Ψn ≡ j ·(v(x)×
·(v(x)× Ψn)
Ψn)
For a given magnetic field the sign of the effect of this marginal operator change is dependent upon the sign of the static twist (chiral handedness) in the spin factor. The coupling produced depends upon the projection of the imposed magnetic field strength onto the axial direction in the atom, but the separation between the two elements of the Bloch space basis also depends upon this angle. Thus the two effects cancel and the frequency of the Rabi gyration in the Bloch space remains independent of this angle. It also accounts for why the Zeeman effect appears with strength of effect and polarisations related to the angle of view from the magnetic field. More notes are due to be added here.
This leads to the Zeeman spectral line splitting effect, and it is present as an additional magnetic effect for all values of
It is apparent in this model that the idea of a fixed magnetic moment cannot really be applied to a modal electron with
Effects comparable to those in the Zeeman effect are introduced by the electric field, but because they enter via a perturbation of the real part of the differential operator their first order effect is the same on both spin modes. It is only with stronger fields that a difference comes about; the effects appear as having a quadratic dependence upon the electric field strength.
There is no magnetic moment produced by an S-mode electron regardless of whether it is isolated (i.e. not member of a spin pair), and even under an applied magnetic field. There is just no net circulation of current. However, an effective magnetic moment can arise for an unpaired spin mode if the magnetic field is tapered. Then such orbitals generate either para or dia magnetic dipole moment depending on spin sign (the Stern-Gerlach effect), but that depends upon chirally handed phase gradient induced in the wave function along the axis of the tapered field. This phase twist is induced by the imaginary gradient in the differential operator resulting from the taper in the magnetic field strength.
When a phase twist exists then there is a finite phase velocity, and that leads directly to a group velocity, and hence bodily motion of the modal field as a whole. The equilibrium can then only be found by the electron mode in question biasing its position away from the centre of the atom so as to produce a converse phase gradient to maintain the atom as a coherent whole. Such a distortion of the modes occurs for a uniform magnetic field too, but since it cancels the phase twist there is no net accelerative effect. With a tapered magnetic field that compensation cannot become complete and an accelerative effect remains.
Any asymmetry of overall phase twist in the atom produces a net acceleration. By treating the electron as a separate entity this may alternatively be evaluated in terms of the force needed to hold the offset electron in the atom, but care is then needed in evaluating the development of the joint charge distribution. The electron is not, in the simple sense, distinct from the atom.
This mechanism produces a para or diamagnetic effect depending on spin sense as though there were a magnetic dipole present, but the direction of the dipole always appears as collinear with the magnetic field and oriented in the same sense depending only on sign of spin. That phenomenon cannot be properly modelled by a magnetic dipole.
The explanation of spin filtering phenomena that are reported from the more elaborate forms of the Stern Gerlach experiments currently forms the crux of the evaluation of this model. If the spatial resolution into quantal results is treated according to the rationale of this model then there has to be what is effectively an amplifier manifested in the underlying wave process that is capable of doing that. For the equivalent sorts of effects obtained with electromagnetic radiation (with photons, as they say) that idea is not difficult to support and explain using the ideas of reciprocal couplings, but for the Stern-Gerlach filtering experiments it drives the requirements placed upon the matter wave system to its full stretch. Further development of this and related documents will therefore be devoted to this issue.
Apparently Bohr is quoted as referring to what I am calling quantal resolution as "irreversible classical amplification", that in spirit is sympathetic to the ideas proposed here, but the processes that form the basis of amplification are themselves sub-quantal, and therefore not in every sense what we might choose to call "classical". Perhaps in line with the idea of an underlying deterministic process model with emergent quantal observation the term "irreversible amplification" would be better, though elsewhere I refer to it as "unilateral amplification" in line with the engineering usage.
In this model the electron is undeserving of its identity as simply an electric charge particle; it is equally involved in both electric and magnetic fields. The possibility of a magnetic monopole density does not arise because the nature of the magnetic effect arises originally as a vector, whereas electric charge appears as monopole because it is a scalar product of scalars. The symmetry between electric and magnetic effects that is normally stressed in the Maxwell equations is in this sense redundant and even misleading.
Notice that for any mode that is unpaired with the opposite spin mode the current density has a strong imaginary part, and for any pair of like modes with opposite frequencies these imaginary parts cancel. Notice also that although these imaginary terms in the vector are strong, nevertheless because the mode is circularly symmetrical they are directed radially so there will be no Maxwellian propagative effect for the imaginary part. This imaginary part of electric current cannot be directly observed.
Electromagnetic Emission and Absorption
The basic case of transfer of energy between an electromagnetic radiation field and an electronic modal system involves the De Broglie wave structures of two spatially overlapping electronic modes and the electric and magnetic fields of the radiation. The rôle of the radiation involves its wave gradient, and because of that the simple case is where the effective modal diameter of the roughly spherical electron is less than half a wavelength of the radiation field, so that covers the cases up to X-rays around 1019Hz.
Such low frequencies as those of light (around 0.7×1015Hz) are capable of interactions with the thousands of times higher frequencies of the electron modes near to the Compton frequency (1.2356×1020Hz). Through their wave function products they are only involved with respect to the differences of these high frequencies.
The strength of this basic form of coupling depends upon the approach to a triple frequency coherence between the two electron modes and the radiation. The energy fluctuation is called a Rabi process, and it can be characterised in a three dimensional state space of energies and phases called a Bloch space. The magnitude of the peak energy fluctuations involved varies approximately in inverse proportion to the difference from the ideal frequency coherence condition. Over one half of the phase relationship cycle of the waves at the triplet of frequencies there is a charge conserving energy transfer from the electron mode with higher absolute frequency to the that with the lower with a net increase of energy in the radiation (stimulated emission), and for the other half of the phase relationship the energy flows are the other way (absorption). There is also one more aspect of phase relationship controlling the reactive transfer of energy between the modes (treating the radiation as a mode too), and hence pulling of the electron frequencies and phase shifting the radiation occurs. In all cases the instantaneous rates of transfer into each of the three wave modes involved is proportional to its signed frequency, and there is no net gain or loss of energy from this triple system ... nothing else is involved. There is no such intuitive quantitative model of interaction based upon the idea of the particulate electron.
State Transition Selection Rules
For coupling like this to be possible at all the two electron mode fields must have a dipole distribution of the amplitude of their field product and the axis of that dipole must lie, at least partly, in the transverse field direction of the radiation. The possible alignments of electric and magnetic fields with this product can be evaluated by starting from equation Emode. The coupling can only happen for certain pairs of modes that have a difference of one order in certain groupings of their spherical harmonic modes.
Think of the case where they have a difference of one cycle azimuthally and are the same order axially, that corresponds to a difference of ±1 in the azimuthal mode order, none in the axial order and therefore demands that for matching radial orders there shall also be a difference of one in their principal quantum numbers. We might also consider the alternative in which they have identical azimuthal orders and differ by one axially, and again a difference of one would be needed in the principal quantum numbers to accommodate this. The former of these is a valid coupling but the latter is not. This appears to be because when the mode product dipole is in the single direction of the atomic axis the electric and magnetic fields have cancelling effects whereas in the azimuthal type of product format there is a two dimensional process and they can then add their effects. (I need to do further checking of that specific point, but the basis is pretty clear.)
Thus with this model the possibility or not of electromagnetically induced excitation and coupling between the various mode pairs is made clear in a rather simple way, and through the spatial moment of intensity distribution of a mode pair product the strength of its coupling can be calculated. It is not likely that the nature of these processes could be either grasped mentally or computed with such alacrity using a particulate notion of the electron. What is more we can take such a model farther, such as by suggesting that for higher frequency X-rays it is then presumably possible to reckon a different set of selection rules for couplings via higher order spatial moments of mode pair product cases.
This model for establishing possible state transitions and their coupling strengths can be extended to the substantially different geometries of the electron fields of molecules and crystals.
The manifestation of Hund's rule resulting from spin field form is mentioned elsewhere in this essay, but that and other specifically spin field effects are probably better left to develop elsewhere in the specific context of the nature of spin. See spin.html.
 Appendix D: Coupling Field Integrations
Appendix D: Coupling Field Integrations
Recapping equation E5 from the main text:
| E5 |
We are concerned here with the way that distributed charges and currents act as sources to drive the generation of electromagnetic fields, and how these processes may be represented by integrations over time and space.
The expressions used show vectors serving as divisors in the integrand, and that is an unconventional notation. In this context it means the following.
For the case of the electric vector field (akin to the gradient of an electrostatic potential) the dividend (i.e. numerator) in the integrand is a scalar. It is the charge density. In this case the quotient of the vector division has a magnitude (norm) that is the quotient of the respective magnitudes of dividend and divisor, and a vector quotient direction that is the same as that of the divisor.
For the case of the magnetic vector potential field (i.e. that field of which the curl is the magnetic field) both dividend and divisor in the integrand are vectors. Here the dividend is the current density. In this case the quotient of the vector division has a magnitude (norm) that is again the quotient of the respective magnitudes of dividend and divisor, but the vector quotient direction in this case is that obtained by reflecting the dividend direction about the divisor direction.
In both cases the magnitude of the resulting amplitude contribution to the vector field integral from any given source element to any given field point follows an inverse square law with distance of the source. This reduces to a field with only transverse waves of both electric and magnetic parts that in the Fraunhofer field follows the inverse square law of intensity with distance (i.e. inverse proportion of field stress amplitude). This Fraunhofer field approximation applies at distances much greater than the overall dimensions of the coherent source structure, and this can be seen to be so because then the radiation arrives at such distant points from a very small range of spatial angles.
These formulae can form the basis of numerical computations over a spatial lattice. Also, the propagation properties of these fields are fully defined by the Maxwell system model. However, if greater agility in analysing and computing these relationships is required then improved mathematical definition of the operations involved may be desirable. This points in the direction of mathematical things like division rings over real spaces.
I hope eventually to add some material here developing these ideas with specific relevance to the electromagnetic fields and their driving sources. For the time being the following web site links may be useful. However they are overly general for the purposes here, as is to be expected when the approach is via the maths rather than the concept domain of our model.
Thanks are due to Dave Rusin at Northern Illinois University for this attractive maths resource.
The Mathematical Atlas: Welcome -  http://www.math-atlas.org/welcome.html
http://www.math-atlas.org/welcome.html
The Mathematical Atlas: Product Structures and Division Rings over the Real Numbers -  http://www.math.niu.edu/~rusin/papers/known-math/index/products.html
http://www.math.niu.edu/~rusin/papers/known-math/index/products.html
 Appendix E: Temporal Smoothing of Charge
Appendix E: Temporal Smoothing of Charge
With superposed complex waves at around the Compton frequency (1.2356×1020Hz) the overall picture we visualise is one of scintillating values producing wildly fluctuating values of intensity (squared magnitude). If these were real waves then any locally based way of calculating charge would produce a broad band of cross-modulation effects with beats at lower frequencies and including frequencies up to around twice the Compton frequency. Even a single frequency real wave mode would produce fluctuation of its squared magnitude at twice the modal frequency. However, firstly here we are using complex rather than real wave functions, and secondly the interaction is not based upon simple squaring of magnitude but rather upon the operation of a Hilbert transform.
When interactions occur only under the Hilbert transform as shown in equation EHt or its frequency domain equivalent in Echarge there is no such fluctuation produced either by self interference (squaring) or between waves with differing, particularly widely differing frequencies. In particular superposed terms with closely similar frequencies of opposite signs (i.e. rotating in opposite directions in the complex plane) produce no charge or current fluctuation at all. This possibility is typically counter-intuitive when first encountered, but detailed evaluation of trial cases using either EHt or Echarge will show this to be the case.
Because of this absence of interaction in the charge and current origination process the causal path in the dynamics of quantal state change is determined entirely by the energy (Hamiltonian) of each respective mode and not by its phase, with the exception of processes where the waves are of nearly identical (including having like sign) frequency when the effects of coherence arise and these relatively slow fluctuations can then be large. Although the electronic modes involve very high frequencies nevertheless the fluctuations of this energy, and hence of the charge distribution, are at relatively low frequencies that are algebraic sums of the electronic modal signed frequencies. It is only in the presence of an alternating electromagnetic field that modal energy transfers can occur, and then it is at these relatively low sum frequencies such as those of light wave radiation (green light, for instance, is around 0.7×1015Hz).
It is interesting to see how the charge and magnet origination processes are made smooth in the time dimension by the Hilbert transform but there is no corresponding effect to smooth them in the spatial dimensions. This fits in with matter when viewed in natural units
When the Hilbert transform operates upon a complex function of time it commutes with the complex conjugation operation upon that function. Using this fact and considering a wave function comprising a pair of frequencies we may see that whilst there is no cross term generated for oppositely signed frequencies there is indeed some cross effect when the two terms have like signs of frequency. However, this cross effect is still of zero mean and occurs at high frequencies. It is thus becoming important to try to establish the credentials of EHt through the promising stochastic underlying model (See "Dynamics of Complex Waves" http://wavemodel.org/model/zero.html). Although it produces the right general effects we must ask is it valid, a useful approximation or just bad?
 Appendix F: Mathematical Groups and the Pure Wave Model
Appendix F: Mathematical Groups and the Pure Wave Model
The wave model as developed here does not place reliance upon mathematical group theory for its basic concepts whereas the conventional exposition of quantum mechanics usually does. For certain particular proofs and derivations the group theoretic approach is helpful and this section is introduced to cover those points. Also, for those who are more familiar with the conventional ways of expressing the maths of quantum mechanics these notes may act as a bridge to those ideas.
This section is not offered as an introduction to the ways of using group theory, if one wanted to, in this kind of modelling other than through mentioning some of the relevant technical terms. We are lucky to have a widely available reference source for these issues in the Internet, and particularly in Wikipedia. Most terms used here can if necessary be looked up by a search using each term as a key word.
Groups that are of interest in wave models
To study general aspects of the transformations of fields and waves that are possible using the Klein-Gordon and Maxwell equations in a model as developed here let us consider the usual group theory ideas of the Lie algebras of the Lorentz and Poincaré groups.
Before launching into that we might note that for the descriptions of behaviour involving unitary transformations between and in perturbations of steady states we are, as usual, concerned with the ideas of the SO(3), SU(2) and SU(3) groups. However these latter notions, though possibly useful as means of handling its applications, are not necessary as means for defining the form of the model. Therefore they are not introduced as definitive precepts, but occasionally mentioned just to link in conventional ideas. They will not be develped further just here.
Excessive richness of particle models
When particles are presumed as fundamental then there is a general tendency for the axiomatic set of the model to proliferate. At least certain very simple models are immediately excluded by such an imposition of entity structure. Putting it simply, whereas a field model without particles is viable (it can develop solitons), there is no such possibility of a particle model without fields (infinitesimal particles cannot interact) ... so a particle basis immediately precludes the more sparsely describable of models.
For example, with particles present as basic then spin structure and the symmetries of time and parity reversal become necessary axioms in the model. In the field continuum model these attributes of behaviour can be shown to arise from nothing more than the inherent invariances of remarkably simple wave equations.
Such burdening of the model with increased axiomatic form leads directly to proliferation of kinds of entities (i.e. the particles themselves) and to substantial compounding of complexity in the process of deriving its behaviour. It is also prone to creating arbitrary mismatches with natural behaviour through the irrelevances of excessive structural specification that are thereby introduced. An example of the latter is the way that the short life of anti-matter is a puzzle in the particle model whereas it is automatically suggested by the recognition of positive and negative values of structural stability characteristics (real parts of poles) in entities of a single kind emergent in the wave model. This kind of entity can be depicted as emergent under interactive wave processes so long a they include mechanisms of observation as modelled upon those same continuum based precepts.
Thus the continuum wave models begin with a prospect of placing less burden upon group theories than is the case for models presuming the additional structures necessary for particles. Our concern is then to investigate what improvements to modelling that prospect might yield.
Simplified Lorentz and Poincaré groups
For the scalar complex field we may restrict our interest in the Lorentz group to its representation of order (0,0), that is the spinless representation. That is because in the model based on the Klein-Gordon equation the phenomena of spin emerge from the topology/mechanics ... they are not introduced as basis concepts. A subsequent application of the spin-bearing representations of Lorentz group theory could still then be considered as a compact way of doing applications analysis of the resulting systems with the spin present, but as such it is no more than a convenience. This approach avoids having to introduce the group theoretic ideas as though they are the fundamental basis ... it leaves the theory based upon structures arising out of a simpler model that may itself be understood in simpler terms, and even visualised at the field level.
The purposes for which symmetry of time and parity reversal are introduced into conventional quantum mechanical theory do not arise in the model developed here. This is because the phenomena calling for those symmetries in the conventional model can be shown to arise under the restricted form of the Lorentz group in this pure wave approach. The resulting further simplification is a significant advantage of this approach to modelling. It occurs through the recognition of both stable and unstable (convergent and divergent) evolutions that arise in processes that are amenable to description within the restricted Lorentz group. No extension from use of the restricted to the full Lorentz group is then needed in the fundamental analysis.
Thus the main simplification appears to be in the omission of the more complicated representations of the Lorentz group. When the resulting spinless restricted Lorentz group is incorporated into the Poincaré group it also inherits this simplification.
It is because of the availability of this simplification that the complex scalar Klein-Gordon wave equation can be used in a class of pure wave models in place of the Schrödinger/Dirac system that is conventionally invoked to describe the matter wave mechanisms generating detection probabilities for particles. Relativity, at least of the "special" variety, is thus incorporated into these continuum models from the outset.
Lorentz invariance
A task necessary to establishing the basis of the wave model developed here is to make clear the invariance of the model under all finite Lorentz transformations of the co-ordinate system. We do not need that any particular quantities shall remain invariant but rather that for every solution of the wave equations in one co-ordinate basis there is just one solution corresponding to it in any other given basis in the Lorentz group. Such is in fact the case for solutions of any system of partial differential equations built on the Minkowski 4-space in which the differentials are all of second order with coefficients forming a self adjoint matrix K with the Minkowski metric in its diagonal elements.
So considering first the Klein-Gordon equation, a change of co-ordinates can be applied to the coefficient array K in the differential operator by pre-multiplying by a matrix C that is unitary under the Minkowski metric and post-multiplying by the inverse of that matrix.
By so doing the corresponding solution is expressed in the transformed co-ordinates. Because that class of matrices for C corresponds to the elements of the Lorentz group and can introduce no singularities in the transformation the necessary invariance is established.
The equation for the free space Maxwell system is even simpler than the Klein-Gordon and complies with the same restrictions in being homogeneous second order. Thus its solutions are similarly invariant. We may use the free space Maxwell equation in this way so long as we check whether there remain any adverse effects of the interactions between the two equation systems.
So we need to establish that the interactions between the two wave systems do not introduce any violations of the lorentz invariance. This follows directly from the appreciation that in the model considered here all interactions between the two wave systems occur only point by point on a local basis. Thus viewed in this way the interactions can be assembled as aggregates of instantaneous mutual effects that occur independently in regions of indefinitely small size. No propagation or distance effects are involved in these individual microscopic interactions, and transformative distortions of co-ordinate values occur in matching ways between the two wave systems, so the invariance survives.
Effect of sign of frequency upon current direction
Both crystalline and free field electronic charge propagation occurs subject to a phase velocity/group velocity mechanism determined by Lorentz invariance and spin is not involved, whereas for bound electron fields in atoms, including those comprising crystals, spin effects create a somewhat different situation in the closed circuits around the spin axis. Because of the composite nature of a spin field additional care is needed to handle the terms with frequencies near to zero.
The sgn(ω) multiplier in the current origination formula Echarge can be applied directly to the non-spin based current origination, both in the free field and in the rectilinear standing wave part of the electron field found in a crystal. In handling solutions of the matter wave equations we must keep separate the excitations of conjugate frequencies. They are independent solutions. We cannot, for instance, consider oppositely signed frequencies to carry the counter flowing currents in an electronic standing wave. The sign of frequency of an electron field cannot be reversed merely by the reflection bounding a standing wave. Rather, any such balance must be achieved by superposing opposite twists in complex argument of two waves with like frequencies passing in the opposite directions. This necessarily induces additive interference such that the standing wave takes on a monophase amplitude modulated form, and hence zero group velocity.
In the case of charge current perturbing the equilibrium of non-spin based electron waves (crystalline or free field charge propagation) the same Lorentz twist associated with propagation adds algebraically to the oppositely signed twist derivatives of any counter flowing terms, thereby producing an imbalance in the opposed terms and therefore an effect of net current flow. In this way the standing wave structure can be viewed as remaining intact as it undergoes the necessary phase twist effects associated with translative motion to comply with the Lorentz invariance.
In the case of the spin fields there are terms with frequencies very close to and varying through zero ... see Wave Topology of a Spin Mode ... and that does not allow a simple application of the "sign of frequency" kind of factor in the evaluation. In particular the zero frequency term with azimuthal twist needs to have such a sign associated with it in order to determine its contribution of current origination. Since the twisted dynamic term naturally takes its own sign of frequency we may try associating the remaining dynamic term, namely the one without twist. This then allows us to evaluate the current derived from these two pairs.
Using the underlying substrate noise field model ... see Dynamics of Complex Waves ... we can see that this is the case because the scattering of the substrate occurs based upon these terms in the spin factor acting together as sums, and it is the pairings of terms with unlike azimuthal twist that produce the systematic summation of effects. Consider for instance the sum of
So it is that reversal of sign of frequency does not alone associate with direction of flow of current. It is the direction of the phase translation that determines the current direction, and that depends upon the product of the wave gradient and the sign of the frequency. The substrate scattering dynamics for this can be modelled in an unequivocal way. Regarding the zero frequency terms involved in spin, by the association with its paired dynamic wave term the static twisted term in a spin factor produces essentially steady current, and hence also magnetic moment, whilst its frequency varies minutely around zero in the process of stabilising operation.
 References and Background Reading
References and Background Reading
This symbol denotes linkage to an independent web site: ![]()
| [ABoDC] | A.G.Booth "Dynamics of Complex Waves" http://wavemodel.org/model/zero.html |
| [ABoES] | A.G.Booth "Essential Structure in Physical Observation" http://wavemodel.org/obs/observ.html |
| [ABoWT] | A.G.Booth "Wave Topology of a Spin Mode" http://wavemodel.org/spin/spin.html |
| [AE87] | L.Allen & J.H.Eberly "Optical Resonance and Two Level Atoms" Dover. 1995 ISBN 0-19-509345-3 Originally published both by General Publishing Co., Ontario and Constable & Co., UK 1975. |
| [HP94] | H.V.Poor "An Introduction to Signal Detection and Estimation." 2nd.Ed. 1994 Springer-Verlag. |
| Phone and e-mail see foot of Wavemodel home page. | ||
| Copyright © A.G.Booth 2004-2005 All rights reserved | ||