 |
Working paper |
| A.G.Booth | WWW original 8 April 2004 | Copyright © A.G.Booth 2004-2006 All rights reserved | ||
| Document ident: | Last updated 22 October 2006 | Wave Topology of a Spin Mode. A.G.Booth | ||
Keys: |
quantized quantization |
|||
This document makes use of the HTML character entities in its text, so if your browser does not support them you will see the raw HTML tags that call them up. I believe that the text should display properly for browser versions starting from v4.5 for Internet Explorer, v6 for Netscape, v6 for Opera and any version of Firefox.
 Summary
Summary
The essay develops how the properties of spin as it is observed in natural microscopic systems can be accounted for in terms of the behaviour of complex waves in space and time. It shows how these wave structures can be visualised and described explicitly.
 Introduction and Motivation
Introduction and Motivation
The idea of spin as applied in quantum mechanics is cloaked in mystery to a greater degree than need be. It is often stated that it is a concept that can only be handled by its mathematical form and not visualised. Here I wish to refute that and show how such a thing as spin can be visualised in quite practical ways, though we must of course use mathematical expressions to quantify any such model and to allow checking of its self consistency in detail.
On the path to a fully locally causal wave theory of physical matter an explicit topological comprehension of spin is needed in terms of wave equation solutions over space and time and these must be adequately determined to be both continuous and finite in their integral of squared magnitude. In spite of widespread belief to the contrary these conditions can indeed be met in wave functions that also display the properties of "spin" nature, but only if (i) the wave variable is complex, and (ii) the use of both positive and negative frequencies is permitted in dynamic models.
The scientific folklore of spin suggests that it cannot be the result of a scalar wave equation. Whilst this is true for a real variable, there is no such impossibility for a complex variable. The conceptual difficulty seems to arise from the quantum models introduced by P.A.M.Dirac where he uses matrix algebra as the means of describing the spin phenomena in a formal manner, thereby appearing to extend the space of the description beyond the possible solutions for complex waves on a Minkowski 4-space. Apparently he did this because it was generally believed that negative frequency could not generate credible solutions in a useful representation of matter particles because according to the Planck proportionality relationship it suggests negative energy states. Reviewing this point we can instead achieve a consistent system in which charge is proportional to modulus of frequency, and then the fully developed locally causal wave model becomes tenable. (Beyond a few remarks that will not be developed in this particular essay ... see the companion essay "Smooth and Quantal Properties ..." smooth.html ).
Apart from a need for some arguably tricky wave topology the problem of apparent unreality in spin is brought about by the insistence upon seeing quantum mechanics in terms of discrete detection mediated by probability waves. This conventionally framed approach creates a conflict between the allusion to particle nature in using a Lagrangian model and the need for positive probabilities of quantal detection. If the model is instead given the form of a truly locally causal wave system then no such inhibition need arise.
Denied the concept of "particle" as fundamental the notion of substance must then be based upon the idea of the soliton ... a stable and persistent wave structure. An Eulerian model of wave process in a continuum can achieve this, and can do so without the non-relativistic and therefore non-local nature of potential as it appears in the Lagrangian model. Instead of potential it is electromagnetic field divergences that play the key role in determining field topology. After all, it is electric field divergence that relates implicitly to charge density, and there is a similar divergence relationship between magnetic vector potential and current density. (Note: This latter use of the word "potential" does not carry with it the relativistic problems of the Coulomb electric potential.) These relationships are Lorentz invariant and therefore relativistically compatible. Using divergence in this way then determines quantal behaviour as an emergent phenomenon in the solutions of the wave model. (See again the companion essay "Smooth and Quantal Properties ..." smooth.html ).
In case you bridle at such apparent heresy, let me assure you that a model with such ubiquitous causality and continuity still leads to the uncertainty principle as necessarily and unavoidably emergent in real observation [ABoES]. However, those ideas will be no more than hinted at within the confines of this essay. Instead only the nature of the spin topology will be developed as a useful and necessary step in that direction and as an interesting idea in its own right.
Possibly the best way to gain an intuitive grasp and visualisation of the structures described herein is to commit to memory the constraints on the possible form of the solution wave functions, and then to allow time to pass whilst dwelling on the thoughts. That certainly is the method that I have used for this subject (and so much time too!). However, that exercise in parallel thinking will not do to define the format of a written document. Instead we need it presented as a logical line of reasoning and defence with a serial format. Still I recommend the use of both approaches if you have the time and inclination. If the going gets tough whilst reading the following I suggest that a meditative interlude of hours, perhaps spread over days, may be of assistance. In so far as your difficulty is the consequence of my bad authorship I apologise.
Tensor formalism is often used for expressing these sorts of field relationships. It is notably powerful in its generalisation, and is frequently used for that reason. However our mission here is not to achieve generalisation at all costs ... indeed I seek rather to make specific descriptions of wave structures in order that a direct visualisation may be achieved. For that reason the main portrayal will be by means of a mixture of verbal descriptions and mathematical expressions for complex functions over three or four dimensional space.
 Establishing a Model
Establishing a Model
We need to introduce to our models the properties of a "spin bearing" wave function. Before making quantitative descriptions of the wave functions I shall discuss broadly some reasons for and constraints on the existence of this phenomenon called spin.
In endeavouring to build these wave models it becomes apparent that the confinement of vibrations or oscillations into localised regions of space does not readily occur. Confinement of wave structures in the usual approach to all kinds of wave modelling with partial differential equations is achieved by the definition of boundary conditions ... in effect walls surround and delimit the region of wave motion of interest. For quantum wave modelling there are no such boundary walls so the localisation effects must be built into the distributed system of interactions so that matter can persist in having localised identity in the form of solitons. The spin construct is the basis on which centres of such identity can be described and accounted for, and around which consistent rules of field interaction can bring about persistent structure of wave processes. This is only possible with a certain kind of singularity at the centre of the localised wave structure and it is the separation of this consideration that concerns us here.
Fortunately the description of the spin topology can be isolated from the other more general aspects of the wave processes. We can define a type of function that carries the spin structure and then apply it to a wave system that is otherwise well defined but spinless. We may define the spin-factor function as that which is to be multiplied with the spinless wave function to produce the complete viable form of a wave mode. The spinless wave function is well behaved in terms of satisfying the wave equation everywhere except at a central singularity that is enforced by the need for circular symmetry. There could arguably, though not in fact feasible, be a spherically uniform symmetry about the central point for a spherical mode (the only simple case of one of those would be in a monatomic hydrogen atom with nothing but its lowest order S-mode excited, but even that is not viable), but for all practical modes (a fortiori the P, D and F-modes) it is a symmetry of positive or negative reflections both in the spherically central point and in the central point in any plane perpendicular to the axis of symmetry.
The reason that spin is needed is for the maintenance of analytic nature of the wave function near the atomic axis. Any wave modal form that cannot accommodate the approach to singular conditions close to the atomic axis whilst still satisfying the definitive wave equation could never persist in existence. We seek a factor of structure applicable to any atomic mode that satisfies this need, and we might well wonder at first whether such a factor could exist.
First we simplify the problem by dealing only with the isolated atom. This has the advantage of leaving all the possible spatial symmetries of the spherical harmonics present and undisturbed. It is permissible because the resulting fields we shall arrive at can produce the full range of less symmetrical alternatives by conformal transformations (ones that maintain the first order form of the local field geometry) to suit constraint by adjacency of other matter. These conformal transformations maintain the system as satisfying the wave equation in spite of its deformations.
Because of the inherent topological properties of a smooth function that is disposed locally about a central point, as must occur in an atom, there are no simple free space standing eigenfunctions that can satisfy the kind of Klein-Gordon wave equation in Minkowski space-time that we need to use for frequencies below the Compton frequency. Thus we seek ways of involving a singularity at the centre and putting together a stable structure in support of it so as to extend our options in synthesising the species of possible solutions. We find that functions with such a singularity can exist, and can have zero value of the complex variable at the singularity too, so that there is no quantitative violation of the wave equation anywhere including at the singularity. It turns out that the zero singularity has to exist at a line rather than a point, as will become evident.
Any harmonic function adequately satisfying bounding by axis and far field convergence and subject to complex argument loop path closure conditions is a candidate as a factor in a wave function since it will not upset the balance of the Klein-Gordon wave equation. The survival of excited states of modal solutions containing such factors in an atomic system depends merely upon their being sufficiently low in their frequency (i.e. in absolute value of imaginary part of modal eigenvalue) to capture a share of the system energy under the equilibrium we call the Fermi distribution. Thus in seeking these integral solutions for modal forms we should consider any harmonic factor functions so long as they help us on the path to finding the ones that contribute to modal viability at the lowest modal energies, which corresponds to the lowest modal frequencies.
The constitutive equations used here take the form of Klein-Gordon and Helmholtz equations with the non differential term expressed as a function of space/time (see equation Emode in smooth.html ). These are not exactly the Schrödinger and Dirac equations as is usual in physics, but are similar, and the solutions of the equations used here in the limit of low velocities and steady complex oscillatory motion correspond, at least in general form, to the solutions of those more conventionally used equations. This change of modelling approach is essentially connected to the more comprehensive wave modelling method to which this account of spin is directed.
There is an unfortunate clash of nomenclature regarding the term "azimuthal" as inherited from the conventions of twentieth century quantum mechanics. In talking of spherical systems with an axis it is proper to use the adjective "azimuthal" to describe patterns, positions and angles in the equatorial plane of the system. In pursuits such as gun aiming and also in wave systems such as are described in antennas and resonators this convention is the one used. Thus the azimuthal order of a spherical harmonic is most naturally associated with the number of cycles of the variable occurring in a circuit around the axis. The harmonic order constituted as the number of half cycles of the variable along the latitude angle from pole to pole would then tend to be referred to as the latitudinal or possibly the axial order. The remaining spherical order is then the radial, being the number of half cycles in the radial form from centre to periphery.
Unfortunately because of the early observation of magnetic quantisation in isolation the term "magnetic quantum number" denoted by
Meanwhile, as a result of spinning top momentum models the term "azimuthal quantum number", but now more commonly called "orbital" or "angular" quantum number and denoted by l (letter L), then became associated in a rather complicated way with what in a wave model would be called the latitudinal (or axial) harmonic order of the wave mode. Here we define this axial harmonic order as the number of half waves along the entire latitudinal angle and denote it as
As a further point of detail, the principal quantum number is what the radial order would be if the other two orders were at their minimum absolute values
Still it is not easy to see how our spin factor will relate to the complicated structures of the spherical harmonics and their convergence to finite integrated energy in the periphery. Nevertheless, we may begin by finding what form of function could satisfy the conditions and therefore be an asymptote for the solution very close to the atomic axis. There we have the benefit of knowing that so long as there is a zero limit at each point on the axis and the function is analytic everywhere else then in the immediate vicinity the field structure will be dominated by the constant field terms in the equation; there will be relatively little charge density to influence things. This simplified equation is then of the ordinary Helmholtz type in three dimensions. (Proof that it does not support a fractional order infinity at the axis with finite total energy remains as a rather tricky challenge!) Given this zero we know from the form of the equation that the field must vary in magnitude in this restricted region as a constant power of the radius. This condition is applicable to each and every electronic mode of the atom. This comes as a possibly unexpected simplification of the boundary condition of the wave at the spherical axis.
 Electron Field Near the Axis
Electron Field Near the Axis
Avoiding the pathological effects of violation of the wave equation at the axis is a problem that is inherently present in any attempt to construct localised solutions without imposed boundaries for the kinds of wave equations that interest us. It appears unlikely that there could be spontaneously maintained stable structures that are not based upon some kind of singularity.
We may usefully commence by studying how the structure, including spin, appears in the small tube of space surrounding the axis in an isolated atom. After all it is the problem of handling the singularity at the atomic axis that gives rise to the need for spin structure in the first place. The ψ-field intensity and hence also charge density become vanishingly small in the immediate vicinity of the axis so that there the wave equations can be evaluated with omission of the charge or current bearing divergence terms. Once the form of the field can be established in this region then it is made easier to see how the presence of distributed charge can overcome the necessarily rising intensity with increasing radius to produce an ultimate convergence towards zero field in the even greater radii.
We might question whether the electron field intensity does really need to, or even in reality does, go to zero at the atomic axis. An intuition to suggest that it does might go as follows. First a singularity appears to be necessary since a localised holomorphic solution without imposed bounds appears not to exist below the Compton frequency and also the signs of some kind of circular structure arise in the natural phenomena called spin. Then symmetry would suggest that any such a singularity must at least involve the axis and probably (hopefully?) nothing more. Further it will never be possible to avoid the pathological effects of such singularities unless they occur at points where the value of the field intensity falls to zero. So we are seeking to construct some kind of a circulative singularity at a zero of the field intensity. To avoid becoming involved in matters of scale in the overall solution we seek functions in this almost unstructured region near the axis that are invariant under changes of scale ... that requires them to have magnitude that takes the form of a real multiplier that is a power law function of the radius. Attempts to do this on a spherical basis about a point zero appear impossible, so that the idea of proposing the zero to exist at a line is forced upon us and is indeed more fruitful.
A similar requirement for a scale free function will prevail in our choice of a multiplicatively separable spin factor function below and the results there will have a bearing on what can or cannot be done in the vicinity of the axis. So before making further study of the field close to the axis let us gain an overview of the nature of candidate functions as the spin factor. The difference is that the spin factor must be a harmonic function (except exactly at the axis) whilst the total field in the axis region need not, so the spin factor is somewhat more restricted.
 Finding the Form of the Spin Factor
Finding the Form of the Spin Factor
To separate from this many facetted study of electron mode forms the issues of building a spin factor we may look at the nature of harmonic functions that can contribute to the construction of realisable fields surrounding a troublesome situation at the axis. So first here are some considerations regarding centro-symmetric solutions.
Harmonic functions in 3-space (and here we are excluding
- In Cartesian co-ordinates:
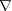 2f(x) = [∂xx + ∂yy + ∂zz]f(x, y, z) = 0
2f(x) = [∂xx + ∂yy + ∂zz]f(x, y, z) = 0
- ... spherical co-ordinates:
[rS2∂rr + 2rS∂r + sec2(φ)∂θθ + (∂φ−tan(φ))∂φ]f(rS, θ, φ) = 0
- ... or cylindrical co-ordinates:
[r2(∂rr+∂zz) + r∂r + ∂θθ]f(r, θ, z) = 0
We need to consider the spin factor as having cylindrical form whereas the quantal ripple function, spherical surface harmonics and radial harmonics too, most naturally inhabit a spherical basis.
Consider a candidate
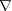 2(f(x).g(x)) = g(x).
2(f(x).g(x)) = g(x).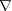 2f(x) + 2(
2f(x) + 2(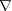 f(x)).
f(x)).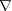 g(x) + f(x).
g(x) + f(x).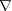 2g(x)
2g(x)
If it is harmonic (except in some way at the centre) so that 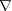 2f(x) = 0
2f(x) = 0
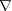 2g(x) + 2(
2g(x) + 2(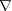 f(x)).
f(x)).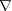 g(x)
g(x)... or equivalently with the spin factor divided out:
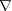 2g(x) + 2(
2g(x) + 2(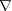 ln(f(x))).
ln(f(x))).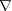 g(x)
g(x)We need a centro-symmetrical function that is harmonic (i.e. produces a zero Laplacian) with a real factor for magnitude that is a constant power law of the radius. It must be real-radial to nullify radial energy transfer and it must be a constant power function of radius to maintain proportionality under scale changes, and in any case to balance constantly any curvature of azimuthal twist that we introduce.
The only such functions with spherical-solid (ball) form have the power of radius either
Cylindrical functions
The only real function with cylindrical form that works is the constant, i.e.
For an amplitude with power ζ of radius as
So a cylindrical form of radial power law harmonic function with azimuthal twist exists, but none of these integer values of ζ can satisfy the requirement that the spin factor, when multiplied into a smooth wave function, shall support necessary convergence at both the z-axis and the far field.
Composite functions
However there are other possibilities by means of dynamically compounding such component functions. A sum of two equal intensity part modes, one flat in the azimuthal circle and the other with complex (cisoid) twist, produces a factor function with the form:
Of the two terms,
The possibility of using different coefficients for these two terms as a means of controlling the strength of the azimuthal twist effect arises. However, a requirement for spectral symmetry also exists (it will enter again here below), and that precludes any such asymmetry of these terms.
Of these two oppositely signed solutions it is the negative one that offers the lower energy wave functions, but to avoid the occurrence of a partial order pole in the wave amplitude at the axis then requires that the axial harmonic order shall never take the value zero.
This appears to leave open a question of whether it is possible to excite any modes based upon the positive solution, and in particular the one with zero axial harmonic order. It suggests the possibility of surd states of ionisation at higher energy.
Additionally for the above solution to work it is required that the two part modes with the same radial ζ power law, though locked together as a unit, shall everywhere be non-interacting. That is effectively possible whilst involving only a given single temporal frequency if one of
This two part composite unit constitutes half of the required structure for a prototypical spin factor.
Conjugate sums build two anti-spin modes
To complete the spin factor requires an additional symmetry of first moment of the spectrum. Study of the substrate field scattering model determines the necessity for this, and it will not be developed here beyond suggesting that it is anyway a fairly intuitive idea once the idea of a substrate noise field is accepted ... see the companion essay Dynamics of Complex Waves .
So two of these composite terms with mutually conjugate frequencies must then be added together, one with its twisted term dynamic and the other with it static. The result is one of a pair of spin modes with like principal (i.e. combined order), magnetic (azimuthal order) and orbital (axial order) quantum numbers. We may then assert a convention that the spin sense of each of these composite modes corresponds to the sign of frequency of its dynamic twisted term. Examples of this composite kind of function in the azimuthal plane for each of the two signs of frequency (i.e. spin senses) can be represented using the alternate signs in:
Let us use the term "spinoid" for either of these modes, and indeed for any topological wave entity with this particular set of symmetries amongst four components. And because these two spinoids are based upon frequencies with opposite signs let us call them an anti-spin pair, or just anti-spinoids. Note that for
Opposite co-spin orientations
Further to all of this, for each of these composite spinoid modes built from four parts there are two oppositely oriented forms with exactly the same quantum numbers, including the ± frequency sense of the spin. The two forms are generated by inversion of the mode in the direction of the spin axis by pivoting about a line laying in the azimuthal mid-plane. That is turning over like flipping a pancake, and is not the same as reflecting in the azimuthal mid-plane. Let us refer to such unmixed spin mode forms that occur as a pair with the same sign of frequency as "co-spinoid modes". For a given spinoid there is just one such pivot line that will position its co-spinoid as orthogonal to it ... due to the half angle effects there is only one orthogonal alignment of co-spinoids in the full circle.
We can recall from Echarge that charge originates as the product of intensity and modulus of frequency, and therefore arises from the dynamic terms, regardless of whether they are twisted. Also it tells us that current originates in the spatial gradient vector and therefore arises from the twisted terms regardless of whether they are dynamic. That may at first appear unintuitive, but it relies on a strict relationship linking existence of each static term with a dynamic term in the constitution of a spin mode.
Thus the basic four component spinoid factor in either of these flipped orientations when multiplied into a static wave function with azimuthal circular symmetry induces azimuthally circular uniform distribution of charge (even though the wave function intensity is not symmetrical in the static parts), and also produces zero current everywhere (balanced between dynamic and static parts). But when any mixture of the two is superposed then that uniformity is lost, even when they are overall orthogonal wave functions. Thus the lowest energy state for an isolated spin mode, due to having least distorted static electromagnetic field, is either one of the pure unmixed spinoid states, not any mixture of the co-spinoid pair.
So long as we set up the convention for positive sense of rotation in the complex plane (+ve frequency) and axial direction convention to determine positive sense of azimuthal complex twist then we may categorise the four components constituting the basic spin factor for mode n at angular frequency ωn and twist order pn as follows:
| Dynamic Twisted ω = ωn, p = pn | Dynamic Flat ω = −ωn, p = 0 |
| Static Flat ω = 0, p = 0 | Static Twisted ω = 0, p = −pn |
As a matter of topological fact the order of azimuthal complex twist p can take any integer values, but for practical electrodynamics purposes we need only consider the lowest energy cases of
Superposition of anti-spin paired modes
When a mixture is made from modes of otherwise identical quantum states by superposition with opposite frequency spin senses, so that we might call this the superposition of "anti-spinoids", then the azimuthal circular symmetry of charge density is again lost. But if first the two contributory anti-spinoids are each built from equal parts of their respective oppositely oriented co-spinoids and the resulting anti-spinoid pair are laid orthogonally in azimuth then the circular uniformity can again be achieved. This produces a rather complicated relationship between the equilibrium states and the possible perturbations from that equilibrium.
Equilibrium states
Isolated spin states at equilibrium are based upon pure spinoids whereas the superposed paired spin states allow two dimensional decomposition into four co and anti-spinoid mixture components. We may convey the amplitudes of mixtures of elements from co or anti-spinoid pairs as angles because for constant modal energy the pairs must vary relatively as cosine and sine functions of an angle-like parameter. But they are not literally angles. Drawn on a two dimensional space with period 2π on both axes the respective positions of the equilibrium modes appear thus:

An isolated spin mode, based on a spinoid, can be perturbed by mixture with parts of its co or anti spinoid forms. A spin pair made up of equally split co-spin mode form and anti-spin mode form can be perturbed from its equilibrium in the same two senses, one the deviation from co-spin balance and the other from anti-spin balance.
Even when at equilibrium the per-mode electromagnetic energy of the paired arrangement with its four half spinoid terms is somewhat increased above that of the isolated spin mode with just one spinoid. This leads to the Hund's rule preference to fill individual spin modes in a given principal quantum number before filling anti-spin pairs. The two dimensional space of disturbance from equilibrium produces the richness of behaviour sufficient to account for the highly characteristic phenomena exhibited in Stern-Gerlach cascaded orthogonal spin filtering experiments.
Inter-mode couplings
The spin compounded electron modes are themselves mutually orthogonal and therefore able to operate independently, but coupling is created by the presence of electromagnetic field at the respective frequency difference of a given pair (including the case of zero frequency difference for a spin pair with otherwise like quantum states). For this to be possible they must have opposite spin senses, difference of modal (quantal) orders such as to give them dipole inner product field, and that dipole must couple to the applied electromagnetic field. In particular a coupling occurs between the members of any symmetrical anti-spin pair at zero frequency under the effect of a static electromagnetic field leading to Zeeman and Stark effects.
 Form of the General Spin Structure
Form of the General Spin Structure
The terms contributing to a spin mode can be assembled in a number of different ways according to the construction of the elements and the choice of pairings of the terms as represented. Having established the outline of the prototype spin functions as explained above, we may collect them into a full expression of a spin based electron wave mode under all its possible configurations in an isolated atom.
Considering
... where we have :
- fS(t, θ)
- Temporal and azimuthal complex spin structure of the mode (amplitude normalised)
- fR(r, φ)
- Radial and latitudinal real structure of the mode (amplitude normalised)
- ml
- Azimuthal order of the mode (the associated magnetic quantum number)
- κ
- A complex multiplier of mode amplitude
The amplitude normalisations of fS and fR are of no basic consequence since they can be compensated by corresponding changes to the constant κ. Solutions of the overall system of equations will, regardless of choice of such normalisation, produce the same level of charge quantisation as related to the unit wave function intensity at unit frequency.
The static structure of
|
Espin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
... where we have :
- t
- Time
- θ
- Azimuthal angular coordinate
- ω
- Modal angular frequency (sign characterised as in its twisted part)
- J
- Spin (anti) mode sense = ±1/2 (spin quantum number)
- p
- Spin mode order (integer)
- α
- Twist (co-spin) azimuthal alignment angle
- β
- Twist (co-spin) inverted superposition phasor
- ξ
- Temporal sinusoid phase
... and amongst several other possibilities it can be expressed alternatively as:
|
||||||||||||||||||||||||||||||||||||||||
 Details Near the Atomic Axis
Details Near the Atomic Axis
Armed with this view of the spin factor we return to the question of the field close to the axis. By determining the minimum conditions for field existence there we can then check to see how the effects of charge can complete the formation of a wave structure convergent at great distance too.
Effect of the nuclear electric field
The positive electric field (negative radial gradient) produced by the nucleus contributes a first order term in the differential operator of the wave equation that results in the ripple solution being spatially phase advanced with respect to the radial co-ordinate. One might wonder whether that will spoil the universal quantising effect of the ripple factor in the wave function. It does not! It is only the electromagnetic divergence terms that can do that, and apart from the very small region inside the nucleus, they are all zero in the region close to the axis.
The inner product of the real radial electric field from the nucleus and the gradient of the wave function has the effect of advancing the radial spatial phase of the quantising ripple function, thereby raising its spatial frequency. However, at equilibrium the ripple function still depends only upon the actual charge distribution (electric field divergence), so although the shape of the field is altered, the rule of quantising to the standard discrete value of charge is not violated. (Questions regarding transient states whilst approaching equilibrium remain interesting and tricky in this respect).
At equilibrium that amounts to concentrating the charge nearer to the nucleus ... it corresponds to the nucleus pulling the electron charge closer. So we may proceed using no electric field as the basis for existence of the mode near to the axis and leave the ripple formation to handle the rest of the problem subject to the conformal transformation of the modal form brought about by the nuclear electric field.
Central cusp
When studying the field close to the axis we are not concerned for the spherical solid harmonic structure of each mode (its radial, azimuthal and axial harmonic orders) so long as there is a first order zero cusp at the axis. The quantising ripple factor produces a zero at the spherical centre point (see "Smooth and Quantal Properties ..." smooth.html ), and the axial harmonic of minimum order one produces zero at all points on the remainder of the axis. The various electron modes all have the same kind of cusp. Their sum also has that much structure too, even if their spin structures are not in azimuthal alignment. In this respect there is much of interest to study in the cases of multiple unpaired magnetic electrons
Unlike the axial (latitudinal) and azimuthal factors of spherical surface harmonics, the radial factor making up the modal structure is not harmonic, but close to the axis we may treat it as harmonic for the above reasons.
Using these constraints on the possible form of the spin factor it is then possible to proceed with analysis of the radial structure of the atom and the mechanism of quantisation, and that will be left for presentation elsewhere (see "Smooth and Quantal Properties ..." smooth.html ).
 Discussion
Discussion
The distinction between the paramagnetic effects and the orbital effects is interesting. The way that an externally applied magnetic field is met by para or diamagnetism is easier to grasp in this field model than is the case with orbiting particle models.
These spin topologies properly predict the observed kinds of spin field effects such as a para/diamagnetic dipole moment with no explicit magnetic moment for a single mode with
The values of the quantal states ml and ms are independent, so the spectral line splitting caused by the coupling via magnetic fields in either direction between orbit ml and spin ms can be calculated in this model. However, because in hydrogen we do not expect a magnetic field either from an electron with
Note in passing, that the existence of this central singularity is logically necessary in that if the eigenmodal wave functions were analytic at all points then they would have no strong effect locking them together. They would be able to wander about with their centroids orbiting each other, and thereby introduce another space for energy to operate. There is no such effect observed. The central singularity can therefore be thought of as a sort of fundamentally constituted rigid pivot or hinge or bearing at the axis of each atom.
 Conclusions
Conclusions
An account of the so-called "spin" effects in physics appears broadly possible in terms purely of causal wave functions, but for its completion depends upon some other aspects of a general wave theory of quantum processes that are not covered herein.
Relationship to the Dirac Spin Model
This description of spin turns out to have strong similarities to that conventionally used in physics where it is explained that every mode can have either of two spins but that each mode can exist for only one sign of frequency. Here we start from two forms of spin as determined by wave function topology, and thereby we get the same number of possible modes as does the conventional Dirac model.
Thus this wave model differs from that used by Dirac in his quantum mechanical equations, but it embraces the same behaviour ... it uses different terms to describe (as far as I have been able to check) an identical underlying system. Thus this model achieves by means of an entirely locally causal wave process what has conventionally been introduced as a purely formal mathematical Ansatz based upon the "spin matrices". Anti-matter remains present in the model as occupying the domain of unstable equilibria. Planck's formula then has to relate energy of the quantum to the modulus of frequency.
 References and Background Reading
References and Background Reading
This symbol denotes linkage to an independent web site: ![]()
| [ABoDC] | A.G.Booth "Dynamics of Complex Waves" http://wavemodel.org/model/zero.html |
| [ABoES] | A.G.Booth "Essential Structure in Physical Observation" http://wavemodel.org/obs/observ.html |
| [ABoSQ] | A.G.Booth "Smooth and Quantal Properties of the Complex Wave" http://wavemodel.org/qed/smooth.html |
| [MW01] |
M.Weiss "Spin."
 http://math.ucr.edu/home/baez/spin/spin.html
http://math.ucr.edu/home/baez/spin/spin.html
|
| [To74] | S.Tomonaga "The Story of Spin." translated T.Oka 1997 Uni of Chicago Press. ISBN 0-226-80794-0 |
| Phone and e-mail see foot of Wavemodel home page. | |
| Copyright © A.G.Booth 2004-2006 All rights reserved |